Istraživanje podataka 2
2025/2026. šk. godina
Pravila pridruživanja
- Podaci predstavljeni u obliku transakcija koje se sastoje od stavki
- Klasičan primer - transakcije iz supermarketa koje sadrže skupove artikala kupljenih od strane kupaca
- Cilj je pronalaženje pravila pridruživanja (tj. povezanost) između grupa artikala koje kupci kupuju
Pravila pridruživanja
- Primer - Analiza teksta
- tekstualni podaci predstavljeni pomoću modela vreća reči (bag-of-words)
- otkrivanje čestih obrazaca može pomoći u identifikaciji termina koje se zajedno javljaju i ključnih reči
- npr. data i mining
Pravila pridruživanja
Ideja i osnovni termini:
- Česti skupovi stavki - pojavljuju se zajedno u određenom broju transakcija
- Na osnovu čestih skupova stavki generišu se pravila pridruživanja oblika \[𝑋⇒𝑌\]
gde su 𝑋 i 𝑌 skupovi stavki
- 𝑋 se naziva telo pravila
- 𝑌 se naziva glava pravila
Pravila pridruživanja
- Najpoznatiji primer: \({Pivo}⇒{Pelene}\)
- Ovo pravilo sugeriše da kupovina piva povećava verovatnoću da će istovremeno biti kupljene i pelene
- Pravila pridruživanja su korisna u različitim primenama ciljanog marketinga
- Primer?
Pravila pridruživanja
- Baza podataka \(T\) sadrži skup od 𝑛 transakcija, označenih sa \(𝑇_1,T_2,…,𝑇_𝑛\)
- Svaka transakcija \(𝑇_𝑖\) definiše se nad skupom stavki 𝑈 dužine 𝑑
Primer
| TID | Skup stavki |
|---|---|
| 1 | {Hleb, Puter, Mleko} |
| 2 | {Jaja, Mleko, Jogurt} |
| 3 | {Hleb, Sir, Jajja, Mleko} |
| 4 | {Jaja, Mleko, Jogurt} |
| 5 | {Sir, Mleko, Jogurt} |
Pravila pridruživanja
- Jedan od oblik zapisa skupa transakcija je tabela dimenzije \(nxd\) gde su redovi transakcije, a atributi stavke iz U
- Svaki atribut je binaran i predstavlja jednu određenu stavku
- Vrednost atributa je 1 ukoliko je stavka prisutna u transakciji, a 0 u suprotnom
- d je obično mnogo veće od prosečnog broja stavki u jednoj transakciji
Primer
| Hleb | Puter | Mleko | Jaja | Jogurt | Sir |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
Pravila pridruživanja
Skup stavki (eng. itemset)
k-skup stavki (k-itemset) je skup stavki koji sadrži tačno k elemenata
Podrška (eng. support) skupa stavki 𝐼 definiše se kao udeo transakcija u bazi podataka 𝑇 koje sadrže 𝐼 kao podskup i označava se sa \(sup(I)\)
Stavke sa visokom korelacijom će se često zajedno pojavljivati u transakcijama i imaće visoku podršku
Problem otkrivanja čestih obrazaca svodi se na određivanje skupova stavki koji zadovoljavaju zadati minimalni nivo podrške
Pravila pridruživanja
Otkrivanje čestih skupova stavki - potrebno je odrediti sve skupove stavki 𝐼 koji se pojavljuju kao podskup u najmanje unapred definisanom udelu minsup transakcija u skupu 𝑇
Niži minsup - veći brojem čestih obrazaca
Previše visok minsup - nijedan česti skup neće biti otkriven
Pravila pridruživanja
- Kada je neki skup artikala 𝐼 sadržan u transakciji, svi njegovi podskupovi takođe će biti sadržani u toj transakciji
- Podrška bilo kog podskupa 𝐽 skupa 𝐼 uvek će biti bar jednaka podršci skupa 𝐼
- Osobina anti-monotonost podrške Podrška svakog podskupa J skupa 𝐼 najmanje je jednaka podršci skupa stavki 𝐼
\[sup(𝐽)≥sup(𝐼),∀𝐽⊆𝐼\]
Pravila pridruživanja
- Osobina zatvorenje na niže - svaki podskup čestog skupa stavki takođe je čest
- Apriori princip: ako je skup stavki čest, tada su i svi njegovi podskupovi takođe česti
- Ovu osobinu često koriste algoritmi za otkrivanje čestih skupova stavki kako bi se proces pretrage skratio i postigla veća efikasnost
Pravila pridruživanja
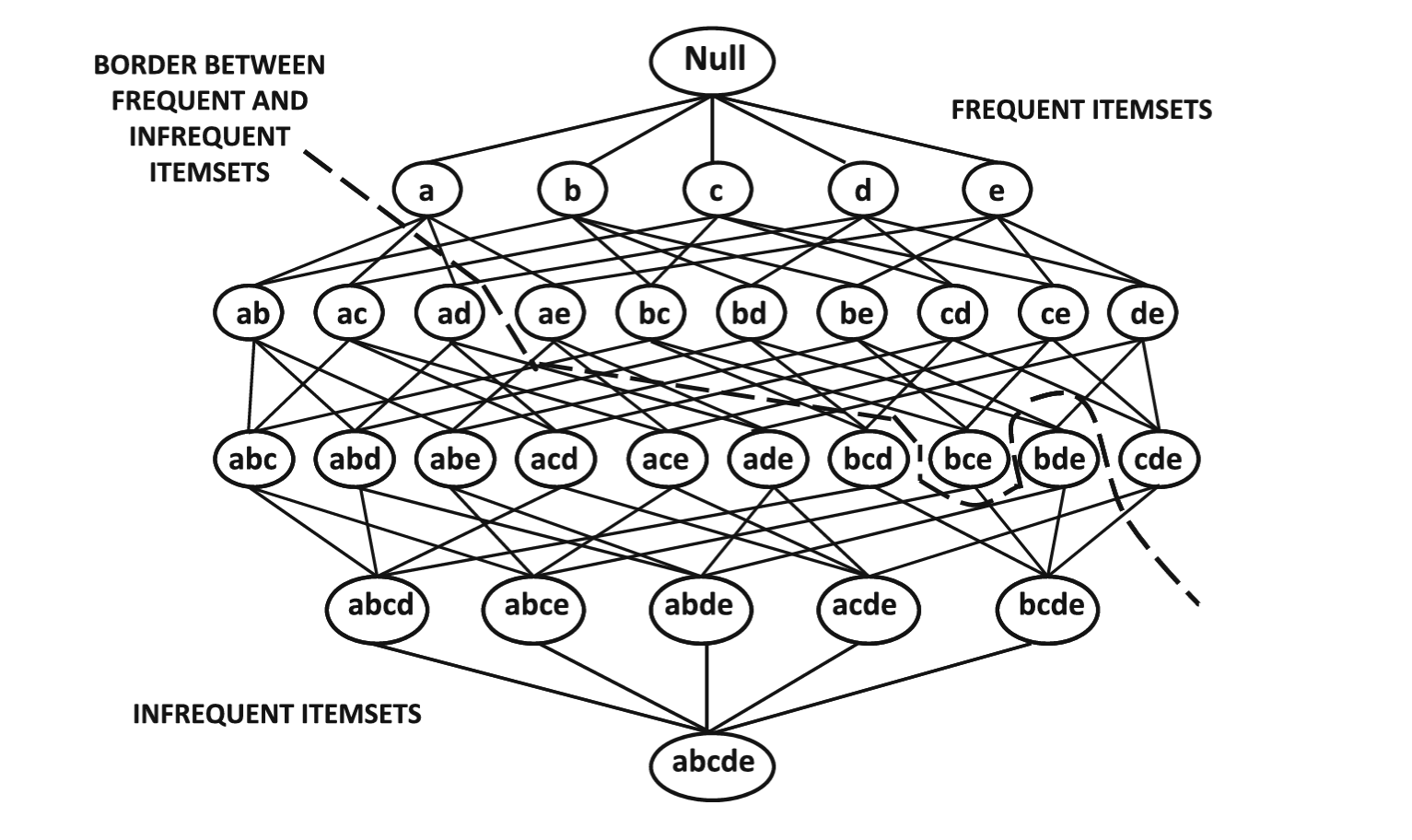
- Skupovi se mogu rasporediti u obliku rešetke skupova stavki
- Rešetka sadrži po jedan čvor za svaki od \(2^d\) skupova formiranih iz 𝑈
- Svi algoritmi za otkrivanje čestih stavki, implicitno ili eksplicitno, prolaze kroz ovaj prostor pretrage kako bi odredili česte obrasce
- Rešetka je granicom podeljena na česte i nečeste skupove stavki
- Svi skupovi stavki iznad ove granice su česti, dok su oni ispod granice retki
Primer
Pravila pridruživanja
Osobina anti-monotonost podrške se može koristiti za formiranje sažetih reprezentacija čestih obrazaca, pri čemu se zadržavaju samo maksimalni česti podskupovi
Maksimalni česti skupovi stavki - čest skup stavki smatra se maksimalnim za datu minimalnu podršku minsup ukoliko je čest i nijedan njegov nadskup nije čest
Ovakva sažeta reprezentacija ne zadržava informacije o vrednostima podrške za podskupove
Maksimalni česti skupovi stavki nalaze se u latici neposredno uz granicu čestih skupova stavki
Pravila pridruživanja
Česti skupovi stavki mogu se koristiti za generisanje pravila pridruživanja korišćenjem mere pouzdanost
Pouzdanost pravila (eng. confidence) Neka su 𝑋 i 𝑌 dva skupa stavki. Pouzdanost pravila \(𝑋⇒𝑌\) označena sa \(conf(X⇒Y)\) predstavlja uslovnu verovatnoću da se skup \(X∪Y\) pojavi u transakciji, pod uslovom da transakcija sadrži skup \(𝑋\)
Pouzdanost pravila \(𝑋⇒𝑌\) definiše se na sledeći način:
\[conf(X⇒Y)=\frac{sup(𝑋∪𝑌)}{sup(𝑋)}\]
Pravila pridruživanja
Pravilo \(X⇒Y\) se smatra zanimljivim pravilom pridruživanja ukoliko zadovoljava sledeće kriterijume
- \(sup(X∪Y)\geq minsup\)
- \(conf(X⇒Y) \geq minconf\)
Pravila pridruživanja
- Celokupan okvir za generisanje pravila pridrusastoji se iz dve faze:
- Generišu se svi česti skupovi stavki za zadat prag minsup
- Generišu se pravila pridruživanja iz čestih skupova artikala za zadat prag minconf
- Prva faza je računarski znatno zahtevnija i stoga predstavlja interesantniji deo procesa, dok je druga faza relativno jednostavna
Pravila pridruživanja
- Neka su \(𝑋_1, 𝑋_2\) i 𝐼 skupovi stavki takvi da važi \(𝑋_1⊂𝑋_2⊂𝐼\). Tada je pouzdanost pravila \(𝑋_2 ⇒𝐼−𝑋_2\) jednaka ili veća od pouzdanosti pravila \(𝑋_1⇒𝐼−𝑋_1\), odnosno:
\[conf(X_2⇒I−X_2)≥conf(X_1⇒I−X_1)\]
- Za pravila {Hleb}⇒{Puter,Mleko} i {Hleb,Puter}⇒{Mleko}, drugo pravilo će imati istu podršku i pouzdanost koja nije manja od pouzdanosti prvog pravila
Algoritmi za otkrivanje čestih skupova artikala
Algoritmi grube sile
Za skup stavki 𝑈 postoji ukupno \(2^d−1\) različitih podskupova, ne računajući prazan skup
Jedna mogućnost bila bi generisanje svih kandidata i brojanje njihove podrške u odnosu na bazu transakcija 𝑇
Algoritmi za otkrivanje čestih skupova artikala
Veća efikasnost algoritama za otkrivanje čestih skupova stavki može se postići primenom jednog ili više sledećih pristupa:
Smanjivanje veličine istraživanog prostora pretrage uklanjanjem kandidata (čvorova rešetke) pomoću osobine zatvorenje na niže
Efikasnije brojanje podrške za svakog kandidata eliminisanjem transakcija koje su poznate kao irelevantne za brojanje podrške datog skupa artikala
Korišćenje kompaktnih struktura podataka za predstavljanje kandidata ili baza transakcija koje omogućavaju efikasno brojanje
Algoritmi za otkrivanje čestih skupova artikala
Pristup zasnovan na gruboj sili može se ubrzati posmatranjem da nijedan skup stavki dužine \(𝑘+1\) ne može biti čest ukoliko neki njegov podskup dužine 𝑘 nije čest - proizilazi iz osobine zatvorenja na niže.
Mogu se enumerisati i brojati podrške svih skupova stavki koji sadrže jednu stavku, zatim dve stavke, i tako dalje, sve dok se za neku dužinu 𝑙 ne desi da nijedan kandidat te dužine nije čest. U tom trenutku proces se može zaustaviti.
Mnogi brzi algoritmi za generisanje skupova stavki koriste osobinu zatvorenja na niže, kako prilikom generisanja kandidata, tako i prilikom njihovog orezivanja pre samog brojanja podrške
Apriori algoritam
Apriori algoritam koristi osobinu zatvorenja na niže kako bi se smanjio prostor pretrage kandidata
Ukoliko je neki skup stavki redak, nema smisla brojati podršku njegovih kandidata–nadskupova
Apriori algoritam najpre generiše kandidate manje dužine 𝑘 i broji njihovu podršku, pre nego što generiše kandidate dužine k+1
Dobijeni česti k-skupovi stavki koriste se za ograničavanje broja kandidata dužine k+1 primenom osobine zatvorenja na niže
Apriori algoritam
- Neka stavke u skupu U imaju leksikografski poredak
- Neka \(F_k\) označava skup čestih k-skupova stavki, a \(C_k\) skup kandidata k-skupova
Algoritam Apriori (Transakcije: 𝑇, minimalna podrška: minsup)
begin
k = 1;
F1 = {svi česti skupovi stavki sa jednim elementom};
while Fk nije prazan
do begin
generiši Ck+1 spajanjem parova skupova artikala iz Fk;
skrati Ck+1 skupove stavki korišćenjem zatvorenja na niže;
odredi Fk+1 brojanjem podrške za (Ck+1, T)
i zadrži skupove stavki iz Ck+1 čija je podrška najmanje minsup;
k = k + 1;
end;
return ∪ Fi;
endPrimer

Apriori algoritam
- Suština algoritma je iterativna petlja koja generiše kandidate dužine k+1 iz čestih k-skupova stavki i broji njihovu podršku
- Kako generisati relevantne kandidate dužine k+1 iz čestih k-skupova stavki u Fk?
- Uvodi se leksikografski poredak i za spajanje se koriste prva 𝑘−1 skupa stavki
- Npr. abcd se dobija spajanjem abc i abd
- Tokom generisanja kandidata dužine k+1 prostor pretrage može se dodatno orezivati proverom da li su svi k-podskupovi kandidata iz 𝐶𝑘+1 sadržani u skupu 𝐹𝑘
- Npr. ako bcd nije čest skup stavki, ni abcd ne može biti —
Apriori algoritam
- Tri glavne operacije algoritma su:
- generisanje kandidata,
- orezivanje i
- brojanje podrške (najskuplje operacija, jer zavisi od veličine baze transakcija 𝑇)
- Broj prolaza kroz podatke jednak je kardinalnosti najdužeg čestog skupa stavki u podacima
Efikasno brojanje podrške
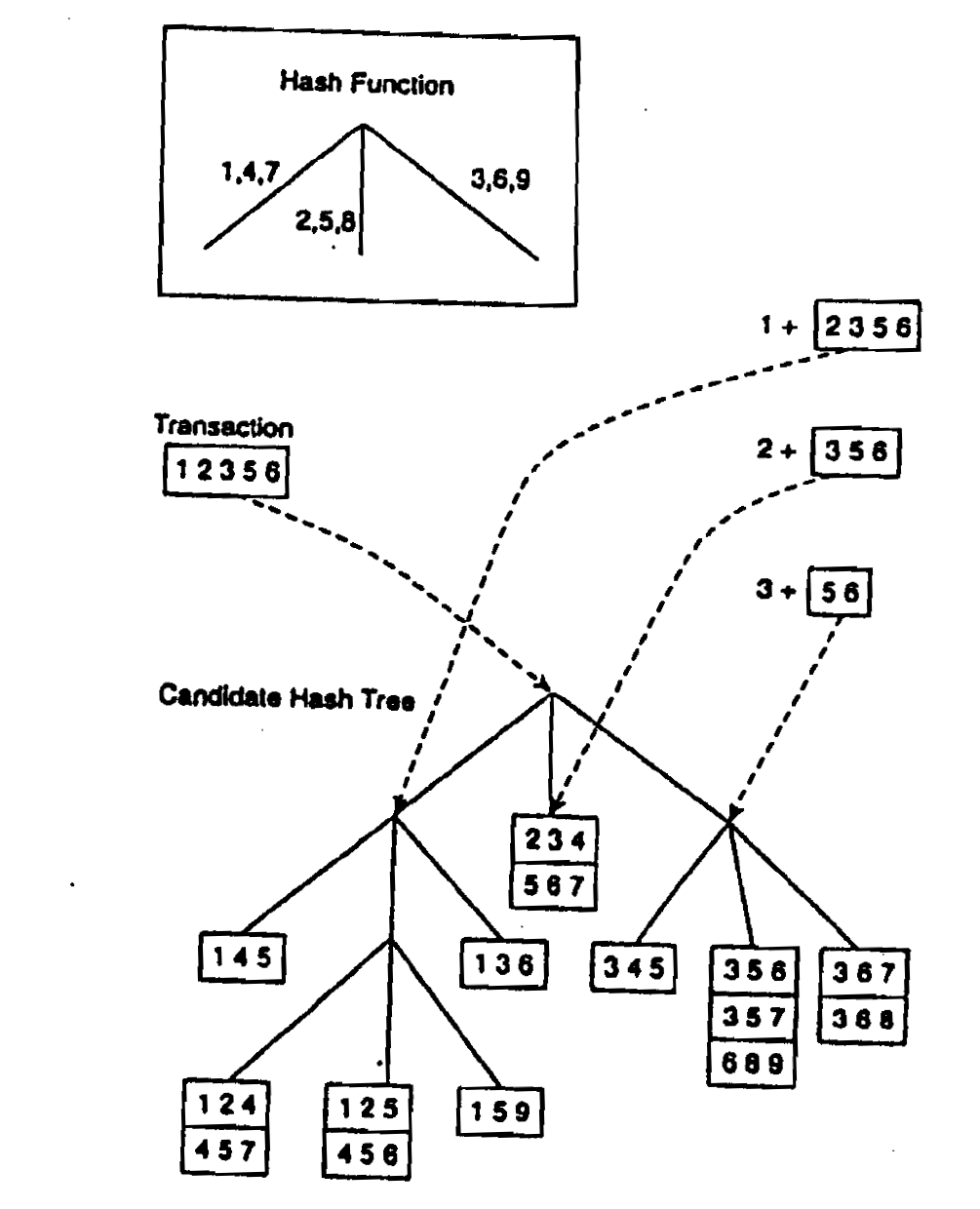
- Heš-stablo se koristi za organizovanje kandidata u skupu \(C_{k+1}\) radi efikasnijeg brojanja
- Pretpostavka je da su stavke u transakcijama i kandidatski skupovi stavki sortirani leksikografskim redom
- Heš-stablo je stablo sa fiksnim stepenom grananja unutrašnjih čvorova
- Svaki unutrašnji čvor povezan je sa heš-funkcijom koja mapira elemente na indekse različitih potomaka tog čvora u stablu
Efikasno brojanje podrške
- List heš-stabla sadrži listu leksikografski sortiranih skupova stavki, dok unutrašnji čvor sadrži heš-tabelu
- Svaki kandidatski skup stavki u \(C_{k+1}\) nalazi se tačno u jednom listu heš-stabla
- Heš-funkcije u unutrašnjim čvorovima koriste se za odlučivanje kojem listu pripada dati kandidatski skup stavki
Efikasno brojanje podrške
- Može se pretpostaviti da svi unutrašnji čvorovi koriste istu heš-funkciju 𝑓 koja mapira u opseg [0,…,h−1]
- Vrednost h predstavlja i stepen grananja heš-stabla
- Kandidatski skup stavki iz \(C_k+1\) mapira se na list stabla definisanjem putanje od korena do lista, korišćenjem heš-funkcija u unutrašnjim čvorovima
- Koren heš-stabla nalazi se na nivou 1, dok se svi naredni nivoi ispod njega uvećavaju za 1
- Pretpostavlja se da su stavke u kandidatima i transakcijama uređene leksikografski
Efikasno brojanje podrške
- U unutrašnjem čvoru na nivou i, heš-funkcija se primenjuje na i-tu stavku kandidatskog skupa \(I∈C_{k+1}\) kako bi se odredilo kojom granom heš-stabla treba nastaviti za taj kandidatski skup
- Kandidatski skupovi stavki u listu čuvaju se u sortiranom redosledu
Efikasno brojanje podrške
- Da bi se izvršilo brojanje podrške, svi mogući kandidatski skupovi stavki u \(C_{k+1}\) koji su podskupovi neke transakcije \(𝑇_j∈T\) pronalaze se u jednom prolazu kroz heš-stablo
- Otkrivaju se sve moguće putanje u heš-stablu čiji listovi mogu sadržati skupove stavki koji su podskupovi transakcije \(𝑇_𝑗\) korišćenjem rekurzivnog obilaska stabla
- Izbor relevantnih listova vrši se rekurzivnim obilaskom na sledeći način
Efikasno brojanje podrške
- Na korenom čvoru prate se sve grane za koje važi da se bilo koja od stavki u transakciji \(𝑇_j\) hešira u odgovarajuću granu. U datom unutrašnjem čvoru, ako je na roditeljskom čvoru heširana i-ta stavka transakcije \(𝑇_𝑗\) , tada se sve naredne stavke u toj transakciji heširaju kako bi se odredili mogući potomci koje treba pratiti
- Prateći sve ove putanje, određuju se relevantni listovi stabla
- Kandidati u listovima stabla čuvaju se u sortiranom redosledu i mogu se efikasno uporediti sa transakcijom \(𝑇_𝑗\) kako bi se utvrdilo da li su relevantni
- Ovaj postupak se ponavlja za svaku transakciju, čime se dobija konačna vrednost podrške za svaki skup artikala u \(𝐶_{k+1}\)
Efikasno brojanje podrške
Vertikalni zapis transakcija
- U vertikalnoj reprezentaciji transakcija T, svaka stavka povezana je sa listom identifikatora transakcija (tid) u kojima se pojavljuje
- Svaka stavka poseduje tid-listu, tj. identifikatore transakcija koje je sadrže
- Ovakva reprezentacija se može posmatrati i kao korišćenje transponovane binarne matrice transakcijskih podataka koja predstavlja transakcije, tako da se kolone transformišu u vrste
Vertikalni zapis transakcija
| Stavka | Skup tid | Binarna reprezentacija |
|---|---|---|
| Hleb | {1,3} | 10100 |
| Puter | {1} | 10000 |
| Sir | {3, 5} | 00101 |
| Jaja | {2, 3, 4} | 01110 |
| Mleko | {1, 2, 3, 4, 5} | 11111 |
| Jogurt | {2, 4, 5} | 01011 |
Vertikalne metode brojanja
- Presek dve tid-liste stavki daje novu tid-listu čija je dužina jednaka podršci odgovarajućeg skupa od dve stavke
- Daljim presekom dobijene tid-liste sa tid-listom neke druge stavke dobija se podrška skupova od tri stavke …
- Npr. presek tid-listi stavki Mleko i Jogurt daje skup {2,4,5} dužine 3. Dalja intersekcija tid-liste skupa sa tid-listom stavke Jaja daje tid-listu {2,4} dužine 2. To znači da je sup({Mleko,Jogurt}) = \(\frac{3}{5}\), dok je podrška skupa sup({Mleko,Jogurt,Jaja}) = \(\frac{2}{5}\)
Vertikalne metode brojanja
- Za par k-skupova stavki koji se spajaju da bi formirali (k+1)-skup, traži se presek njihovih tid-listi kako bi se dobila tid-lista rezultujućeg (k+1)-skupa
- Ovakav pristup naziva se rekurzivni presek tid-listi
Vertikalna verzija Apriori algoritma
begin
k = 1;
F1 = {svi česti skupovi stavki sa jednim elementom};
konstruši vertikalne tid-liste za svaku čestu stavku;
while Fk nije prazan
do begin
generiši Ck+1 spajanjem parova skupova stavki iz Fk;
ukloni iz Ck+1 skupove stavki koji krše osobinu zatvorenja na niže;
generiši tid-listu svakog kandidatskog skupa iz Ck+1 presekom
tid-listi para skupova iz Fk koji je korišćen da se kandidat dobije;
odredi podrške skupova iz Ck+1 koristeći dužine njihovih tid-listi;
Fk+1 = česti skupovi iz Ck+1 zajedno sa njihovim tid-listama;
k = k + 1;
end;
return ∪Fi;
endVertikalne metode brojanja
- Vertikalni Apriori algoritam je računarski efikasniji od horizontalnog Apriori algoritma, ali je memorijski zahtevniji zbog potrebe da se uz svaki skup stavki čuvaju odgovarajuće tid-liste
Apriori algoritam zasnovan na particionisanju
- Apriori algoritam zasnovan na particionisanju zahteva samo dva prolaza kroz bazu transakcija
- Baza transakcija se deli na međusobno disjunktne particije, od kojih je svaka dovoljno mala da može stati u raspoloživu glavnu memoriju
- U prvom prolazu, algoritam čita svaku particiju i izračunava lokalno česte skupove artikala za svaku particiju
- U drugom prolazu, algoritam broji podršku svih lokalno čestih skupova stavki u odnosu na kompletnu bazu podataka
Apriori algoritam zasnovan na particionisanju
- Ako je neki skup stavki čest u odnosu na kompletnu bazu podataka, on mora biti čest u najmanje jednoj particiji
- Zbog toga se u drugom prolazu kroz bazu transakcija računa učestalost samo onih skupova stavki koji pripadaju uniji svih lokalno čestih skupova stavki
- Ovaj drugi prolaz direktno određuje sve česte skupove stavki u bazi podataka kao podskup prethodno definisane unije
Algoritam FP rasta
- Kodira skup transakcija primenom kompaktne strukture podataka FP-drvo i izdvaja česte skupove stavki direktno iz ove strukture
- Frequent Pattern (FP)
- FP-drvo se konstruiše jednim prolazom kroz transakcije
- Svaka transakcija se mapira u putanju
- Kako različite transakcije mogu imati nekoliko istih stavki, njihove putanje se mogu preklapati
- Nivo kompresije zavisi od toga koliko se putanje preklapaju
Konstrukcija FP drveta
- Na početku postoji samo koren (null) drveta
- Jednim prolazom kroz skup podataka određuje se podrška svake stavke
- Česte stavke su sortirane prema podršci u opadajućem redosledu - F-lista
- Stavke koje nisu česte se zanemaruju
- Drugim prolazom kroz skup transakcija pravi se FP-drvo
- Za svaku transakciju
- sortiraju se stavke prema redosledu u F-listi
- mapira se u putanju u drvetu
Konstrukcija FP drveta
- Zajednički prefiksi transakcija dele iste grane (čvorove)
- Svaki čvor u stablu sadrži
- naziv stavke sa brojačem koji pokazuje broj transakcija mapiran u tu putanju i
- pokazivač ka najbližem čvoru sa “desne” strane koji ima istu oznaku stavke radi bržeg pristupa čvorovima koji sadrže istu stavku
- Ukoliko putanja za datu transakciju već postoji, brojači zajedničkih čvorova duž te putanje se uvećavaju
- Nove stavke dovode do pravljenja novih potomaka
Konstrukcija FP drveta
- Pravi se i zaglavna tabela koja povezuje svaku stavku iz F-liste sa njenim prvim pojavljivanjem u stablu čime se omogućava brz pristup svim čvorovima koji sadrže datu stavku
- Veličina FP-drveta je obično manja od veličine nekoprimovanih podataka jer transakcije obično dele nekoliko stavki
- Veličina FP-drveta zavisi i od toga kako su stavke sortirane
Primer
| TID | Stavke |
|---|---|
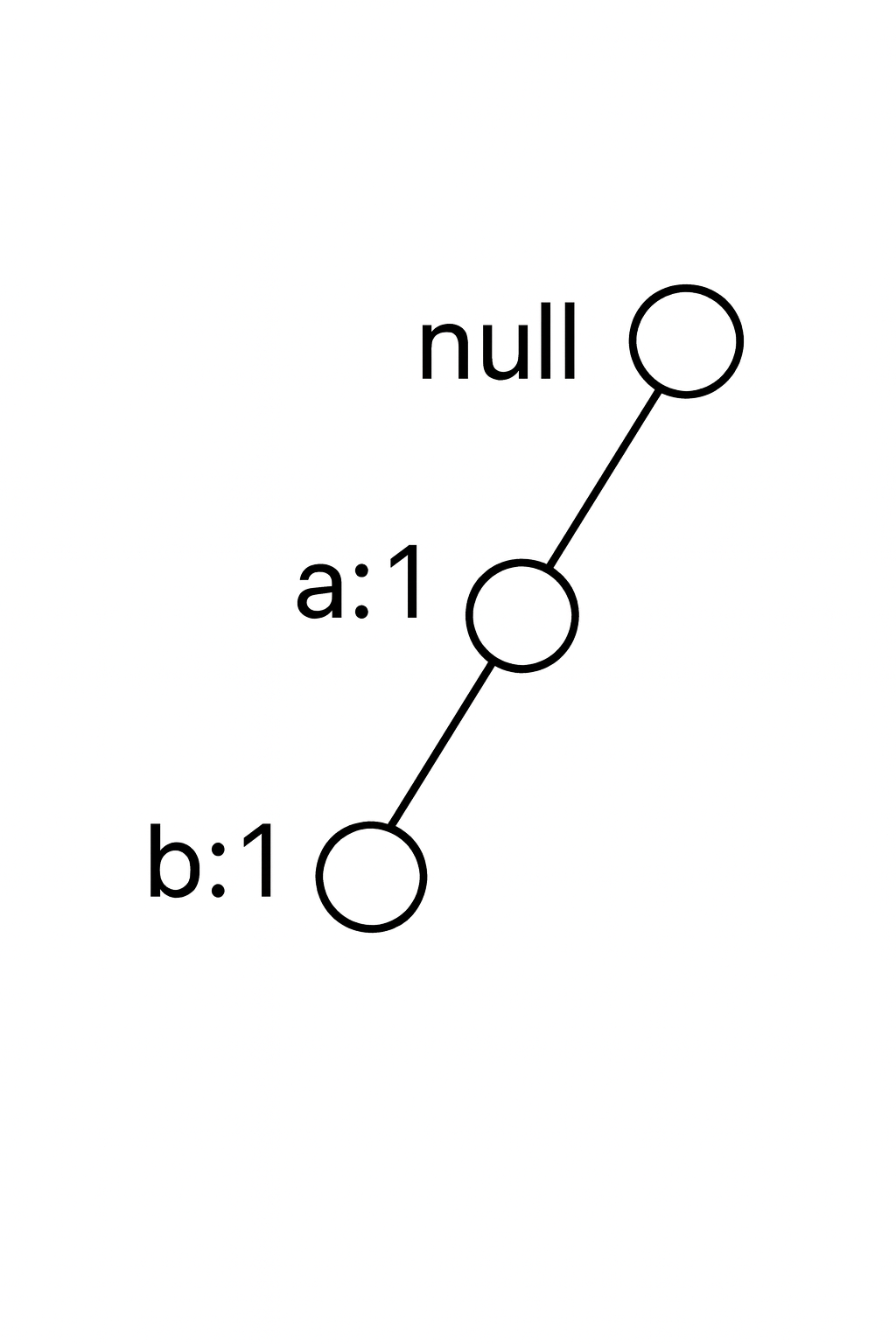
| 1 | {a, b} |
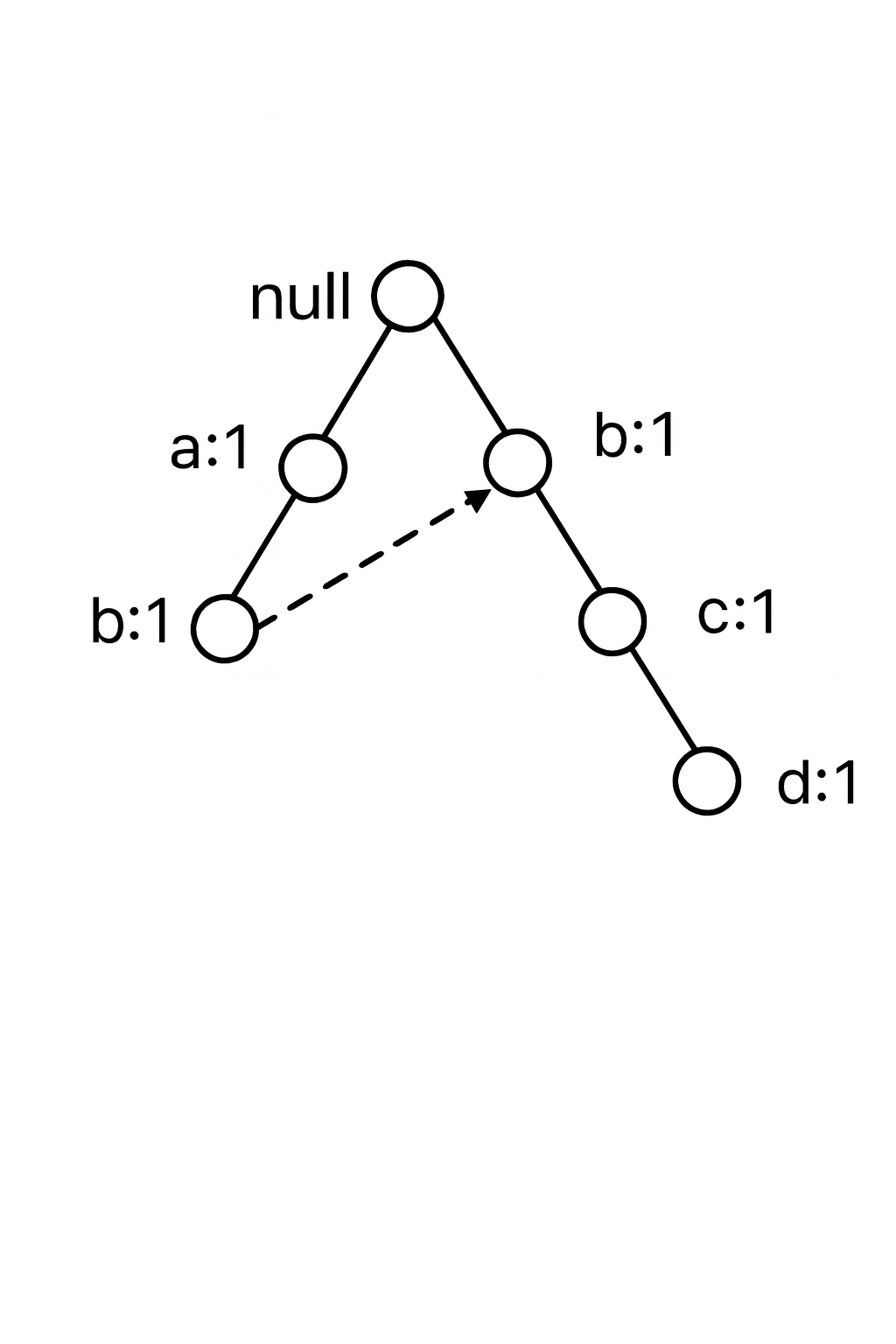
| 2 | {b, c, d} |
| 3 | {a, c, d, e} |
| 4 | {a, d, e} |
| 5 | {a, b, c} |
| 6 | {a, b, c, d} |
| 7 | {a} |
| 8 | {a, b, c} |
| 9 | {a, b, d} |
| 10 | {b, c, e} |
Primer
FP-drvo posle čitanja TID=1
Primer
FP-drvo posle čitanja TID=2
Primer
FP-drvo posle čitanja TID=3
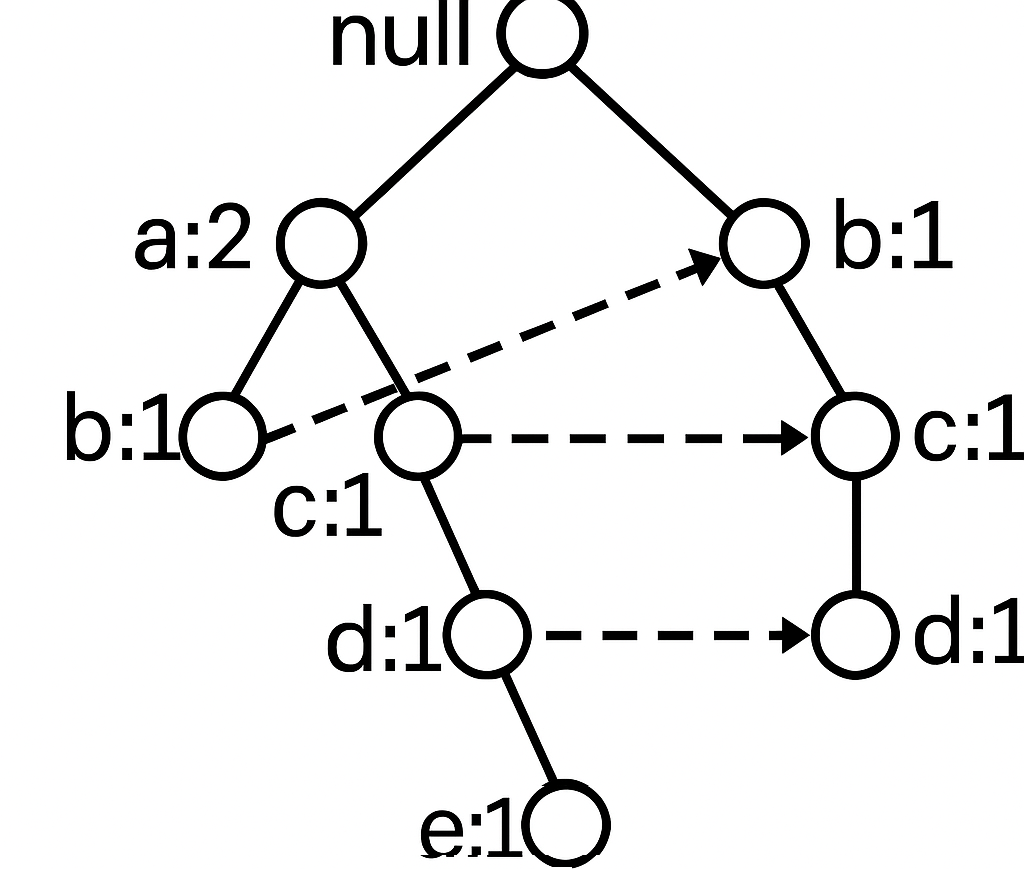
Primer
FP-drvo posle čitanja TID=10
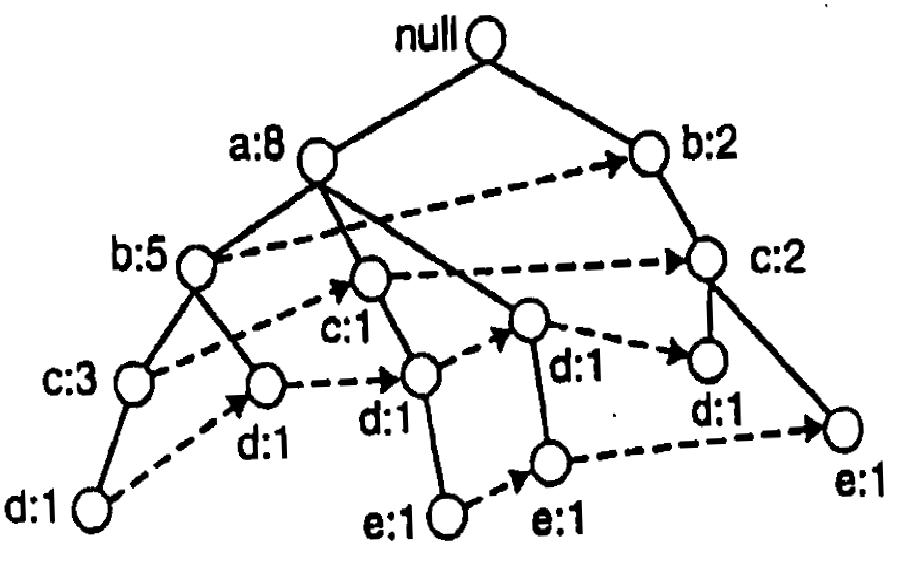
Algoritam FP rasta
- Algoritam FP rasta pronalazi česte skupove stavki iz FP-drveta obrađujući drvo od listova ka korenu, tj. od dna ka vrhu
- Algoritam pronalazi sve česte skupove stavki sa određenim sufiksom primenom zavadi pa vladaj strategije radi podele problema na manje potprobleme
Algoritam FP rasta
- Zadaje se minimalna podrška minsup i FP-drvo
- Obrađuju se stavke od najmanje česte ka najčešćoj, tj. prema F-listi
- Za stavku 𝑖 pronalaze se sve putanje koje vode do 𝑖 - drvo sa prefiks putanjama koje se završavaju sa i
- Od prefiks putanja se pravi uslovno FP-stablo tako što se uklanjaju čvorovi za stavke koje u tom podstablu ne zadovoljavaju minsup
- Česti obrasci dobijaju se tako što se trenutna stavka 𝑖 kombinuje sa svim čestim stavkama pronađenim u njenom uslovnom FP-stablu; postupak staje kada je uslovno stablo prazno ili sadrži jednu putanju.
Algoritam FP rasta - primer
- F-lista = [a,b,c,d,e]
- minsup = 2
- Prvo se traže česti skupovi stavki koji se završavaju sa e
- Izdvajaju se prefiks putanje koje se završavaju sa e
Algoritam FP rasta - primer
Prefiks putanje koje se završavaju sa e
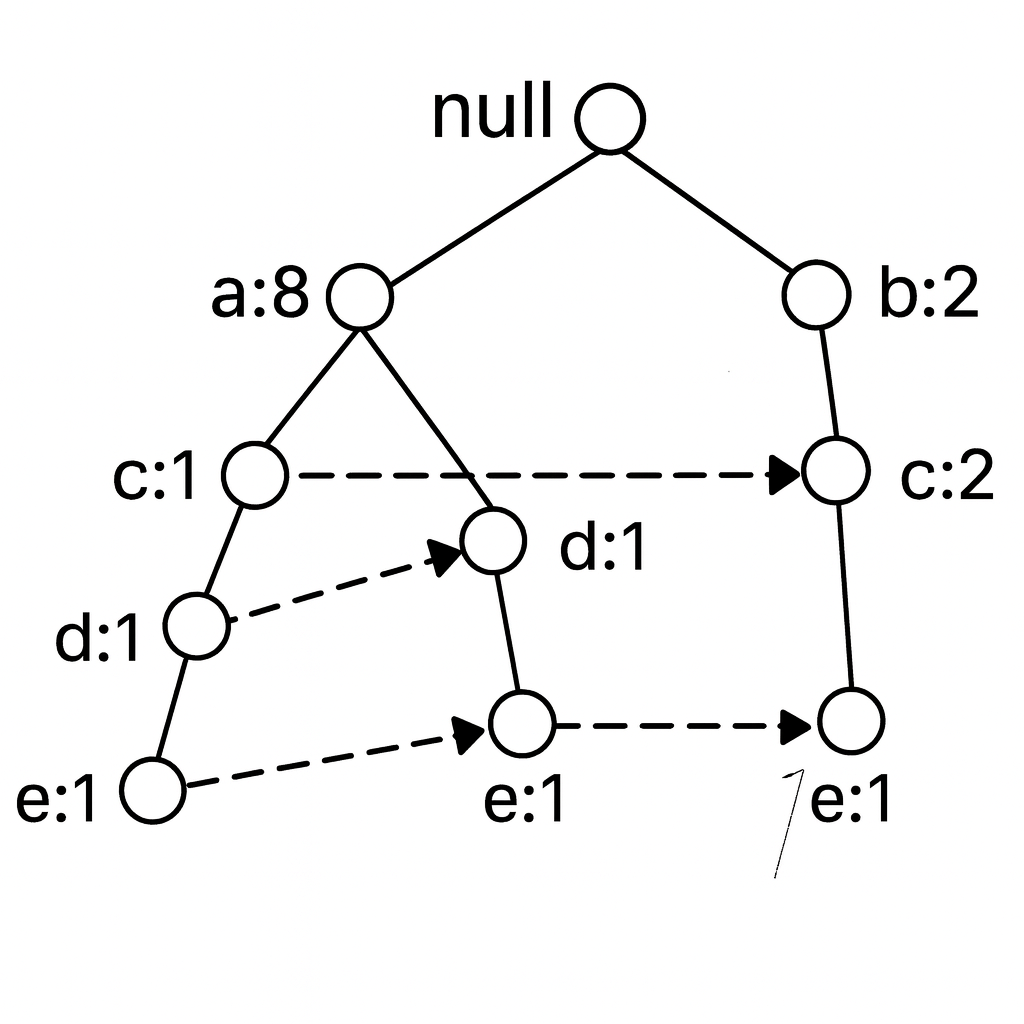
Algoritam FP rasta - primer
- sup(e) = 3 te je e čest skup
- Pravi se uslovno FP-drvo:
- brojači podrške u prefiks putanjama se ažuriraju jer neki sarže transakcije koje ne sadrže stavku e - {b,c} ne sadrži e
- iz prefiks putanja se uklanjaju čvorovi za e
- uklanjaju se čvorovi iz prefiks putanja za stavke koje nisu česte - stavka b
Algoritam FP rasta - primer
Uslovno FP-drvo za e
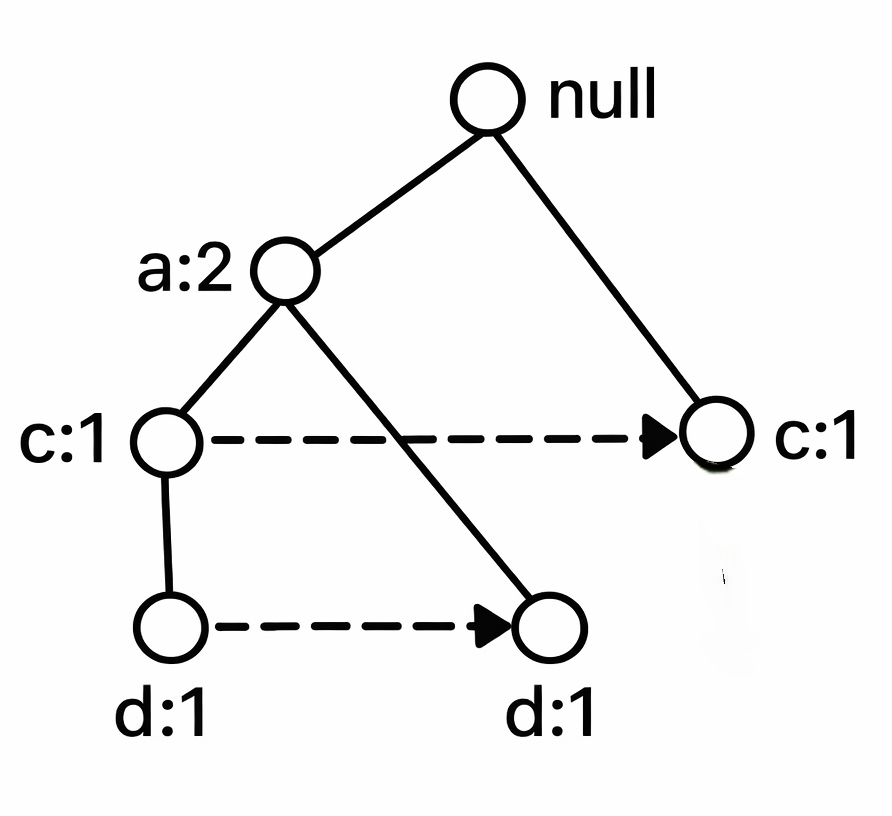
Algoritam FP rasta - primer
- Rešavaju se potproblemi - traženje čestih skupova stavki koji se završavaju sa de, ce i ae
- Za pronalaženje čestih skupova koji se završavaju sa de, prefiks putanje za d se dobijaju korišćenjem uslovnog FP-drveta za e
Algoritam FP rasta - primer
Prefiks putanje koje se završavaju sa de
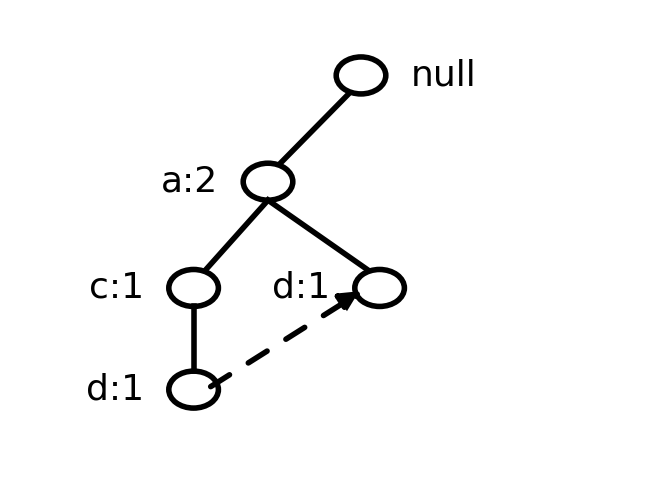
Algoritam FP rasta - primer
Računa se podrška za de računanjem podrške za d u dobijenom stablu
sup({d,e})= 2 te je čest skup
Pravi se uslovno FP-drvo za de
c nije čest te se uklanja
Algoritam FP rasta - primer
Uslovno FP-drvo za de
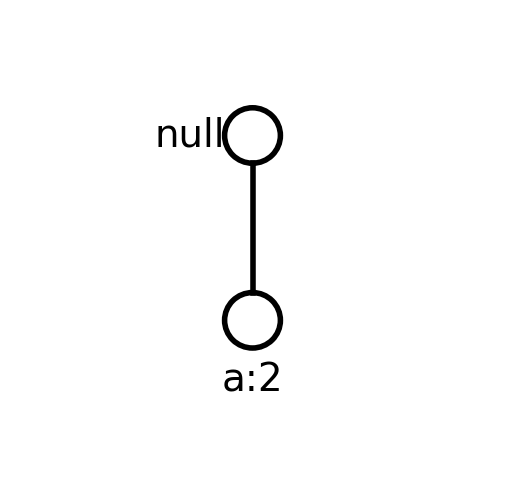
Algoritam FP rasta - primer
- Kako uslovno FP-drvo sadrži samo jednu stavku a sa podrškom 2, algoritam izdvaja čest skup {a,d,e} i prelazi na sledeći potproblem, generisanje čestih skupova stavki koji se završavaju sa ce
Algoritam FP rasta - primer
- Obradom prefiks stabla za c, samo je {c,e} čest skup
Prefiks putanje koje se završavaju sa ce
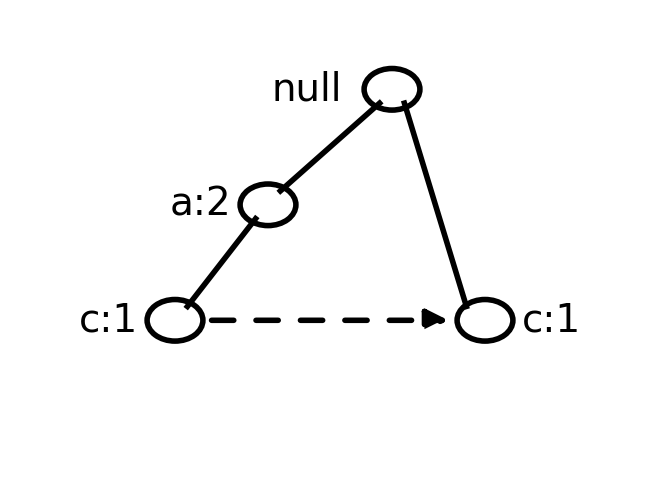
Algoritam FP rasta - primer
- Obradom prefiks stabla za a, uočava se da je samo {a,e} čest skup
Prefiks putanje koje se završavaju sa ae
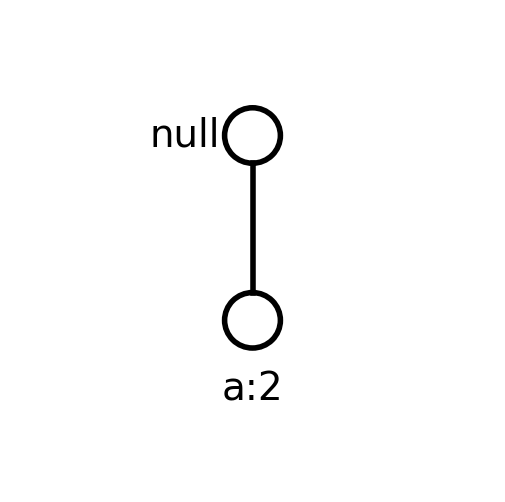
Algoritam FP rasta - primer
Lista svih čestih skupova stavki
| Sufiks | Česti skupovi stavki |
|---|---|
| e | {e}, {d,e}, {a,d,e}, {c,e}, {a,e} |
| d | {d}, {c,d}, {b,c,d}, {a,c,d}, {b,d}. {a,b,d}, {a,d} |
| c | {c}, {b,c}, {a,b,c}, {a,c} |
| b | {b}, {a,b} |
| a | {a} |
Dodatne mere za proveru pravila
- Tradicionalni model za generisanje čestih skupova stavki je široko popularan zbog svoje jednostavnosti, tj. jednostavnog računanja podrške i pouzdanosti
- Međutim, ovako pronađena pravila (samo na osnovu podrške i pouzdanosti) nisu uvek značajna iz perspektive primene
- Pravila koja u glavi sadrže skup stavki koje se pojavljuju u svim transakcijama nisu zanimljiva iako im je pouzdanost 100%
Dodatne mere za proveru pravila
- Zanimljive su mere koje otkrivaju negativne obrasce
- Vrednost 0 u binarnoj matrici tretira se na način kao i vrednosti 1, tj. prisustvo i odsustvo stavke se tretira na sličan način
- Za ovakve mere se kaže da ispunjavaju bit-simetrično svojstvo
- Npr. posmatraju skup stavki \((Pelene, Pivo)\), kao i \((\neg Pelene, \neg Pivo)\)
Lift mera
- Mera koja koriguje nedostatak pouzdanosti i uzima u obzir i podršku glave je Lift mera
\[Lift(X \Rightarrow Y) = \frac{conf(X \Rightarrow Y)}{sup(Y)}\]
- Ako je Lift>1 - glava pravila se češće pojavljuje u transakcijama u kojima se pojavljuje telo pravila nego u transakcijama koje je ne sadrže
- Pravilo \(X \Rightarrow Y\) je zanimljivo ako je \(Lift(X \Rightarrow Y) \ne 1\)
Koeficijent korelacije
\[ρ_{ij} = \frac{sup({i, j}) − sup(i) · sup(j)}{\sqrt{sup(i) · sup(j) · (1 − sup(i)) · (1 − sup(j))}}\]
- Koeficijent korelacije ima vrednost u opsegu \([−1,1]\)
- Vrednost +1 označava savršenu pozitivnu korelaciju, dok vrednost −1 označava savršenu negativnu korelaciju
- Vrednost bliska 0 ukazuje na slabo korelisane podatke
- Mera zadovoljava bit-simetrično svojstvo
Jakardov koeficijent
Jakardov koeficijent (eng. Jaccard coefficient)
Liste identifikatora transakcija (tid liste) u jednoj koloni mogu se posmatrati kao skupovi, a Jakardov koeficijent između dve tid liste može se koristiti za izračunavanje njihove sličnosti
Neka su \(𝑆_1\) i \(𝑆_2\) dva skupa
Jakardov koeficijent se računa na sledeći način:
\[𝐽(𝑆_1,𝑆_2)=\frac{∣𝑆_1∩𝑆_2∣} {∣𝑆_1∪𝑆_2∣}\]
Jakardov koeficijent
- Jakardov koeficijent se može generalizovati na više skupova
\[𝐽(𝑆_1,…,𝑆_k)=\frac{∣⋂𝑆_i∣}{∣⋃𝑆_𝑖∣}\]
- Kada skupovi \(𝑆_1,…,𝑆_𝑘\) odgovaraju tid listama 𝑘 stavki, presek i unija tid lista mogu se koristiti za određivanje brojioca i imenioca formule
Jakardov koeficijent
Moguće je koristiti minimalni prag Jakardovog koeficijenta kako bi se odredili svi relevantni skupovi stavki
Jakardove značajnosti zadovoljava svojstvo skupovne monotonosti. Naime, k-strani Jakardov koeficijent \(J(S_1,…,S_k)\) uvek je veći ili jednak (k+1)-stranom Jakardovom koeficijentu \(𝐽(𝑆_1,…,𝑆_{𝑘+1})\)
Brojilac Jakardovog koeficijenta se monotonо ne povećava sa porastom vrednosti 𝑘, dok se imenilac monotonо ne smanjuje.
Jakardov koeficijent ne može rasti sa povećanjem vrednosti 𝑘
Jakardov koeficijent
- Kada se primeni minimalni prag na Jakardovu značajnost skupa stavki, dobijeni skupovi stavki takođe zadovoljavaju svojstvo zatvoranja na niže
- Većina tradicionalnih algoritama, kao što je Apriori mogu se relativno lako generalizovati za korišćenje Jakardovog koeficijenta
Sažeta reprezentacija obrazaca
Algoritmi za otkrivanje čestih skupova stavki često pronalaze veliki broj čestih skupova
Većina generisanih čestih skupova je često redundantna
Postoje različite vrste kompaktnih reprezentacija koje zadržavaju različite nivoe informacija o stvarnom skupu čestih obrazaca i njihovim vrednostima podrške
Sažeta reprezentacija obrazaca
- Najpoznatije reprezentacije su maksimalni česti skupovi stavki i zatvoreni česti skupovi stavki
- Zatvorene reprezentacije su u potpunosti bez gubitka informacija u pogledu podrške i pripadnosti skupova stavki
- Maksimalne reprezentacije su sa gubitkom informacija u pogledu podrške, ali bez gubitka informacija u pogledu pripadnosti skupova stavki
Maksimalni česti skupovi stavki
Čest skup stavki je maksimalan za minsup ako je čest i ako nijedan njegov nadskup nije čest
Podrška pravih podskupova maksimalnog skupa stavki uvek je jednaka ili strogo veća od podrške samog maksimalnog skupa, što je posledica svojstva monotonosti podrške
Primer

Maksimalni česti skupovi stavki
- Jedan način za kompresiju čestih skupova stavki jeste otkrivanje isključivo maksimalnih skupova stavki
- Preostali skupovi stavki mogu se izvesti kao podskupovi maksimalnih skupova stavki
- Iako se svi skupovi stavki mogu dobiti iz maksimalnih skupova stavki korišćenjem pristupa zasnovanog na podskupovima, njihove vrednosti podrške se ne mogu rekonstruisati
- Maksimalni skupovi stavki su reprezentacija sa gubitkom informacija, jer ne zadržavaju informacije o vrednostima podrške
Zatvoreni skup stavki
- Skup stavki 𝑋 je zatvoren ako nijedan njegov nadskup nema potpuno istu podršku kao 𝑋
- Neka je 𝑋 zatvoreni skup stavki, a \(S(X)\) skup njegovih podskupova sa jednakom podrškom
- Za svaki skup stavki \(𝑌∈𝑆(𝑋)\), skup transakcija \(T(Y)\) koje sadrže 𝑌 je potpuno isti
- Algoritam za otkrivanje zatvorenih čestih skupova stavki vratiće samo skup 𝑋 iz skupa \(S(X)\)
- Skup stavki \(𝑋\) je zatvoreni česti skup stavki pri minimalnoj podršci minsup ako je istovremeno zatvoren i čest
Otkrivanje sekvencijalnih obrazaca
- Problem otkrivanja sekvencijalnih obrazaca može se posmatrati kao vremenski analog problema otkrivanja čestih skupova stavki
- Većina algoritama za otkrivanje čestih skupova stavki može se prilagoditi za otkrivanje sekvencijalnih obrazaca
- Problem otkrivanja sekvencijalnih obrazaca definiše se nad skupom od N sekvenci. i-ta sekvenca sadrži \(𝑛_𝑖\) elemenata u određenom vremenskom redosledu
- Svaki element sadrži skup stavki
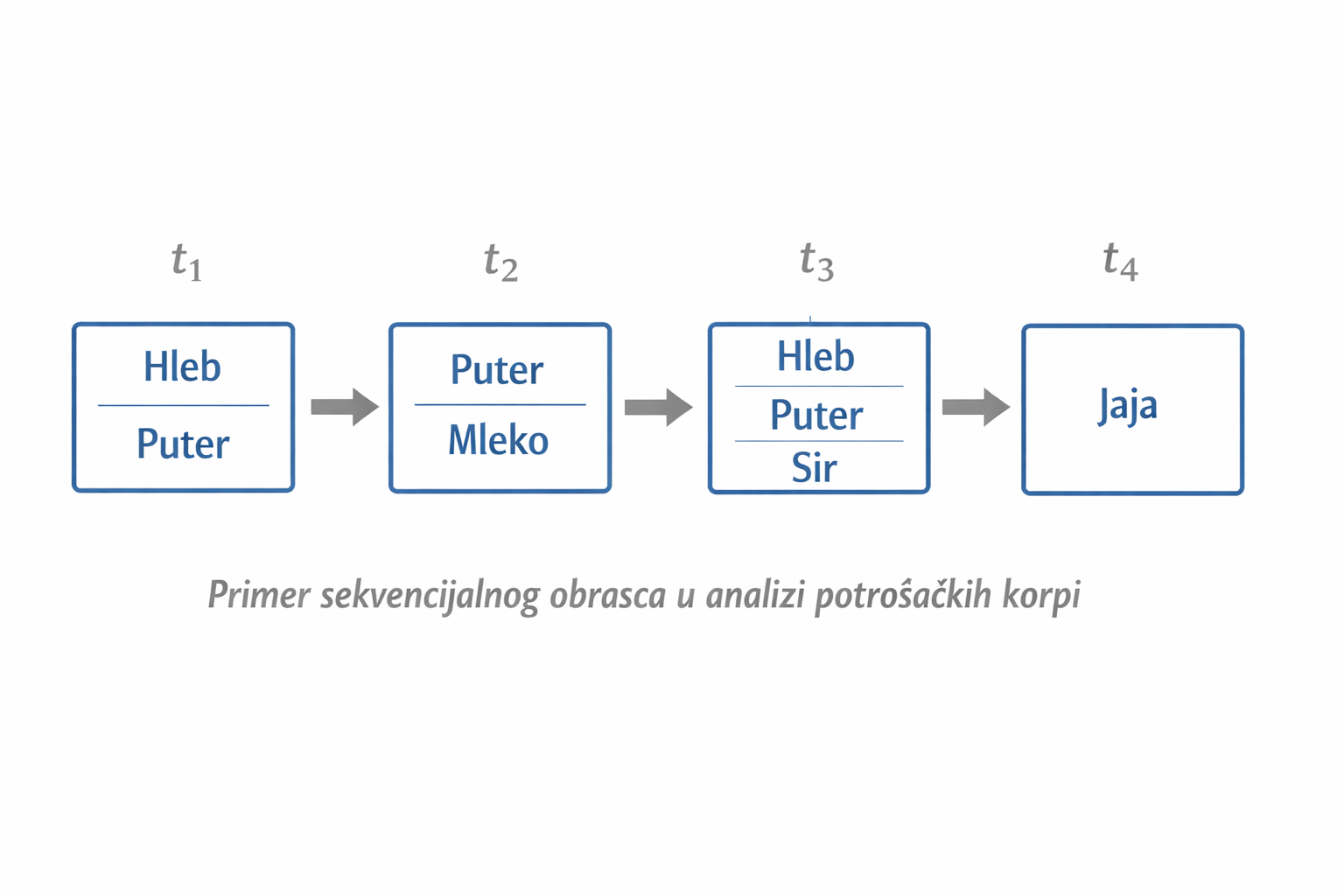
- Npr. sekvenca ⟨{Hleb, Puter},{Puter, Mleko},{Hleb,Puter,Sir},{Jaja}⟩
- {Hleb, Puter} je jedan element, dok je Hleb stavka unutar tog elementa
Primer
Otkrivanje sekvencijalnih obrazaca
- Podsekvenca sekvence je vremenski uređen niz skupova, takav da je svaki element podsekvence podskup nekog elementa osnovne sekvence, uz očuvanje istog vremenskog redosleda
- Transakcije su neuređeni skupovi, dok sekvence (kao i podsekvence) sadrže uređenje (i potencijalno ponovljene) elemente, od kojih je svaki sam po sebi sličan transakciji
- Podsekvenca: Neka su \(𝑌=⟨𝑌_1,…,𝑌_𝑛⟩\) i \(𝑍=⟨𝑍_1,…,𝑍_𝑘⟩\) dve sekvence, pri čemu su svi elementi \(𝑌_𝑖\) i \(𝑍_𝑖\) skupovi. Sekvenca 𝑍 je podsekvenca sekvence 𝑌 ako se u sekvenci 𝑌 može pronaći k elemenata \(𝑌_{𝑖_1},…,𝑌_{i_𝑘}\) takvi da važi \(𝑖_1<𝑖_2<⋯<𝑖_𝑘\), i ako za svako \(𝑟∈{1,…,𝑘}\) važi \(𝑍_𝑟 ⊆ 𝑌_{𝑖_𝑟}\)
Otkrivanje sekvencijalnih obrazaca
- Podrška podsekvence 𝑍 definiše se kao udeo sekvenci u bazi 𝑇 koje sadrže 𝑍 kao podsekvencu
- Otkrivanje sekvencijalnih obrazaca: Potrebno je odrediti sve podsekvence čija je podrška u odnosu na bazu 𝑇 bar minsup
Otkrivanje sekvencijalnih obrazaca
- Prvi algoritam za otkrivanje sekvencijalnih obrazaca bio je Generalized Sequential Pattern Mining (GSP), algoritam sličan Apriori algoritmu
- Dužina kandidata ili česte sekvence jednaka je ukupnom broju stavki (a ne elemenata) u sekvenci
- k-sekvenca \(⟨𝑌_1,…,𝑌_r⟩\) je sekvenca za koju važi: \(\sum_{𝑖=1}^𝑟∣𝑌_𝑖∣=𝑘\)
- Npr. sekvenca ⟨{Hleb,Puter,Sir},{Sir,Jaja}⟩ predstavlja kandidata dužine 5, iako sadrži samo 2 elementa
- (k−1)-podsekvenca k-kandidata može se generisati uklanjanjem jedne stavke iz bilo kog elementa u k-sekvenci
- Apriori svojstvo važi i za sekvence, jer svaka (𝑘−1)-sekvenca k-sekvence ima podršku koja je bar jednaka podršci same k-sekvence
Algoritam GSP
- \(k \leftarrow 1\)
- \(F_k \leftarrow\) skup svih čestih 1-sekvenci
- Dok \(F_k\) nije prazan:
- Generiši \(C_{k+1}\) spajanjem parova sekvenci iz \(F_k\), tako da uklanjanje jedne stavke iz prvog elementa jedne sekvence odgovara sekvenci dobijenoj uklanjanjem jedne stavke iz poslednjeg elementa druge sekvence;
- Odbaci kandidate \(C_{k+1}\) koji krše zatvorenje na niže;
- Odredi \(F_{k+1}\) prebrojavanjem podrške kandidata iz \(C_{k+1}\) i zadrži česte sekvence;
- \(k \leftarrow k + 1\)
- Vrati \(\bigcup_{i=1}^{k} F_i\)
Algoritam GSP
- GSP algoritam započinje generisanjem svih čestih 1-sekvenci (\(F_1\)) jednostavnim prebrojavanjem pojedinačnih stavki
- U narednim iteracijama konstruiše se skup kandidata \(C_{k+1}\) spajanjem parova sekvencijalnih obrazaca iz skupa \(F_k\)
- Bilo koji par čestih k-sekvenci \(𝑆_1\) i \(𝑆_2\) može se spojiti ako je sekvenca dobijena uklanjanjem jedne stavke iz prvog elementa sekvence \(𝑆_1\) identična sekvenci dobijenoj uklanjanjem jedne stavke iz poslednjeg elementa sekvence \(𝑆_2\)
Algoritam GSP
- Npr. dve 5-sekvence \[𝑆_1=⟨\{Hleb,Puter,Sir\},\{Sir,Jaja\}⟩\] i \[𝑆_2=⟨\{Hleb,Puter\},\{Mleko,Sir,Jaja\}⟩\]
mogu se spojiti, jer uklanjanje stavke Sir iz prvog elementa sekvence \(𝑆_1\) daje istu sekvencu kao uklanjanje stavke Mleko iz poslednjeg elementa sekvence \(𝑆_2\)
Algoritam GSP
- Da je \(𝑆_2\) 5-kandidat sa tri elementa, odnosno \(S_2=⟨\{Hleb,Puter\},\{Sir,Jaja\},\{Mleko\}⟩\), spajanje bi takođe bilo moguće
- Sledeća pravila mogu se koristiti za izvršavanje spajanja:
- Ako je poslednji element sekvence \(𝑆_2\) jednočlani skup, tada se spojeni kandidat dobija dodavanjem poslednjeg elementa sekvence \(𝑆_2\) u sekvencu \(𝑆_1\) kao poseban element.
- Npr. za \(𝑆_1=⟨\{Hleb,Puter,Sir\},\{Sir,Jaja\}⟩\) i \(𝑆_2 =⟨\{Hleb,Puter\},\{Sir,Jaja\},\{Mleko\}⟩\), njihov spoj je: \(⟨\{Hleb,Puter,Sir\},\{Sir,Jaja\},\{Mleko\}⟩\)
Algoritam GSP
- Ako poslednji element sekvence \(𝑆_2\) nije jednočlani skup, već je nadskup poslednjeg elementa sekvence \(𝑆_1\), tada se spojeni kandidat dobija zamenom poslednjeg elementa sekvence \(𝑆_1\) poslednjim elementom sekvence \(𝑆_2\)
- Npr. za \(𝑆_1 =⟨\{Hleb,Puter,Sir\},\{Sir,Jaja\}⟩\) i \(𝑆_2=⟨\{Hleb,Puter\},\{Mleko,Sir,Jaja\}⟩\) njihov spoj je: \(⟨\{Hleb,Puter,Sir\},\{Mleko,Sir,Jaja\}⟩\)
Algoritam GSP
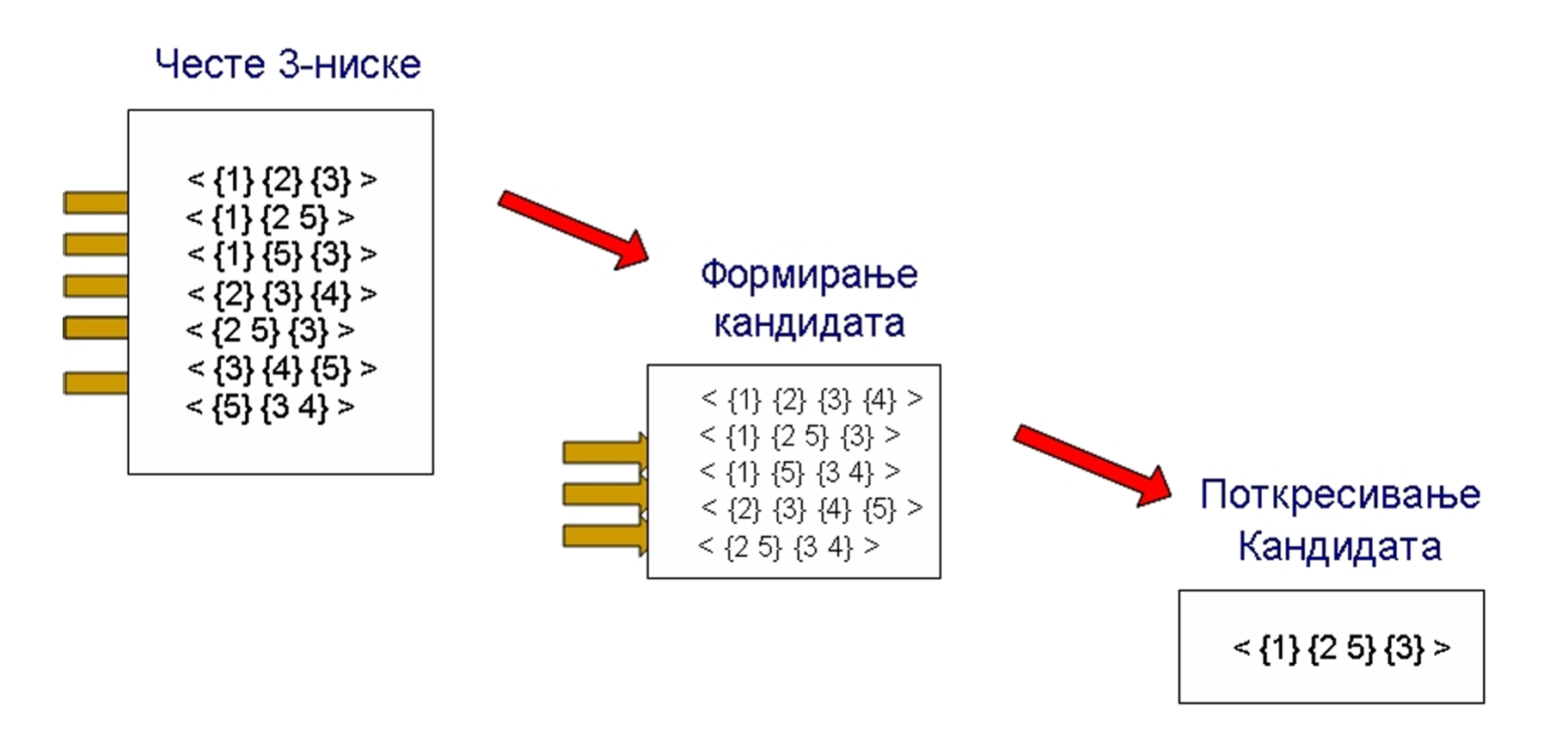
- Nakon generisanja kandidata primenjuje se Apriori trik za orezivanje sekvenci koje krše svojstvo zatvorenja na niže
- Ideja je da se proveri da li je svaka k-podsekvenca kandidata iz skupa \(𝐶_{𝑘+1}\) prisutna u skupu \(𝐹_𝑘\)
- Kandidati koji ne zadovoljavaju ovo svojstvo uklanjaju se iz skupa kandidata
- Preostali kandidati u \(𝐶_{𝑘+1}\) se proveravaju u odnosu na bazu sekvenci 𝑇, pri čemu se izračunava njihova podrška
- Svi česti kandidati iz skupa \(𝐶_{𝑘+1}\) zadržavaju se u skupu \(𝐹_{𝑘+1}\)
Algoritam GSP
- Algoritam se zaustavlja kada se u nekoj iteraciji ne generišu nove česte sekvence u skupu \(𝐹_{𝑘+1}\)
- Kao rezultat, algoritam vraća sve česte sekvence generisane tokom različitih iteracija
Primer
Otkrivanje sekvencijalnih obrazaca sa ograničenjima
- Za sekvencijalne obrasce mogu se postaviti ograničenja
- Npr. ograničenja na razmake između uzastopnih elemenata sekvence
- Ograničenja mogu da se uključe u GSP
- Ograničenja se eksplicitno proveravaju tokom prebrojavanja podrške
- Uključivanje ograničenja može dovesti do narušavanja svojstva zatvorenja na niže
Otkrivanje sekvencijalnih obrazaca sa ograničenjima
- Kada svojstvo zatvorenja na niže nije narušeno, GSP algoritam se može koristiti uz veoma male izmene, koje se svode na proveru ograničenja tokom prebrojavanja podrške
Ograničenja
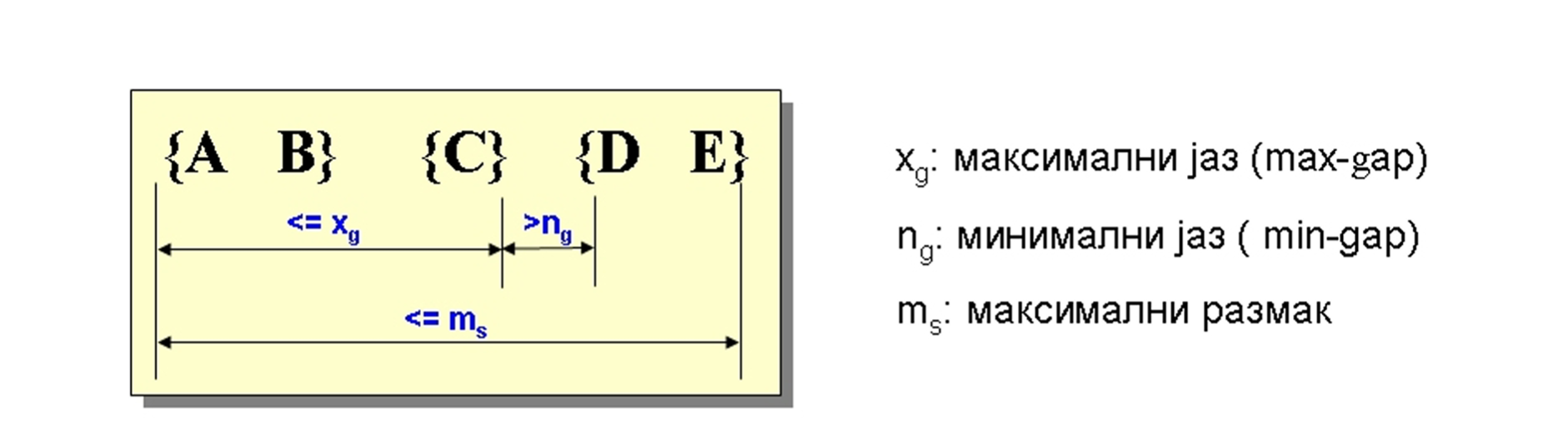
- Ograničenje koje ne narušava svojstvo zatvorenja na niže je ograničenje maksimalnog razmaka (eng. maxspan)
- ograničenje zahteva da vremenska razlika između prvog i poslednjeg elementa podsekvence ne bude veća od vrednosti maxspan.
Primer
Ograničenja
- Ograničenje maksimalni jaz (eng. maximum gap), koje se naziva i maxgap ograničenje
- Sve (k−1)-podsekvence nekog čestog k-niza ne moraju biti validne zbog ovog ograničenja
- Problem - Apriori princip ne može se efikasno primeniti
- Npr. podsekvenca \(𝑎_1𝑎_5\) nije podržana sekvencom \(𝑎_1𝑎_2𝑎_3𝑎_4𝑎_5\) za vrednost maxgap=1, jer je razmak između jednak 3
- Npr. podsekvenca \(𝑎_1𝑎_3𝑎_5\) jeste podržana sekvencom \(𝑎_1𝑎_2𝑎_3𝑎_4𝑎_5\) za vrednost maxgap=1,
- Moguće je da podsekvenca \(𝑎_1𝑎_5\) ima manju podršku od podsekvence \(𝑎_1𝑎_3𝑎_5\), te se Apriori orezivanje ne može primeniti.
Ograničenja
- Sekvenca dobijena uklanjanjem stavki iz prvog ili poslednjeg elementa česte sekvence uvek će biti česta
- Može se koristiti modifikovano pravilo orezivanja. Prilikom provere (k−1)-podsekvenci kandidata radi orezivanja, proveravaju se samo one podsekvence koje sadrže isti broj elemenata kao kandidat.
- Elementi koji sadrže jednu stavku ne mogu se uklanjati iz kandidata prilikom provere njegovih podsekvenci. Takve podsekvence nazivaju se kontigvnim (uzastopnim) podsekvencama.
Ograničenja
- Ograničenje minimalnog razmaka (eng. minimum gap), odnosno mingap ograničenje, između uzastopnih elemenata
- zadovoljava svojstvo zatvorenja na niže te se GSP pristup može koristiti uz proveru ovog ograničenja tokom prebrojavanja podrške. Time se generiše manji skup podsekvenci \(𝐹_𝑘\)
Literatura
- Charu C. Aggarwal: Data Mining The Textbook, Springer, 2015.
- glave 4 i 5