Istraživanje podataka 2
2025/2026. šk. godina
Klasterovanje
- Dati skup objekata podeliti ih grupe (klastere) koje sadrže veoma slične objekte
- Izvršiti podelu datog skupa objekata \(X=\{x_1,x_2,...,x_n\}\) na grupe tako da je objekat \(x_i\) koji pripada grupi \(G_l\) sličniji po nekom kriteriju objektima \(x_j\) koji pripadaju istoj grupi \(G_l\) nego objektima koji pripadaju drugoj grupi \(G_m\). Svaka od grupa G se naziva klaster, a postupak podele ulaznog skupa klasterovanje.
Algoritmi zasnovani na predstavnicima
- Svaki klaster ima svog predstavnika koij ga opisuje (npr. objekat iz skupa, centroid, …)
- Oslanjaju se na mere bliskosti kako bi grupisali objekte
- Kada su predstavnici klastera određeni, nere bliskosti se koristiti da se objekti iz skupa dodele njihovim najbližim predstavnicima
Algoritmi zasnovani na predstavnicima
- Broj klastera (k) zadaje korisnik
- Neka je D skup podataka koji sadrži n objekata (tačaka) podataka označenih sa \(\{x_1,x_2,...,x_n\}\) u d-dimenzionom prostoru. Cilj je odrediti k predstavnika \(\{y_1,y_2,...,y_k\}\) koji minimizuju ciljnu funkciju O:
\[𝑂=\sum_{𝑖=1}^𝑛min_𝑗Dist(x_𝑖,y_𝑗)\]
- Potrebno je minimizovati zbir rastojanja različitih tačaka podataka do njihovih najbližih predstavnika
Algoritmi zasnovani na predstavnicima
GeneričkiAlgoritamZasnovanNaPredstavnicima
(Baza podataka: D, Broj predstavnika: k)
begin
Inicijalizuj skup predstavnika S;
repeat
Formiraj klastere (C₁, …, Cₖ) tako što se
svaka tačka podataka x ∈ D dodeljuje
svom najbližem predstavniku iz skupa S
koristeći funkciju rastojanja Dist(·, ·);
Ponovo formiraj skup S određivanjem po jednog
predstavnika yⱼ za svaki klaster Cⱼ tako da se
minimizuje
∑ {xᵢ ∈ Cⱼ} Dist(xᵢ, yⱼ);
dok se ne postigne konvergencija;
vrati (C₁, …, Cₖ);
endAlgoritmi zasnovani na predstavnicima
Algoritam započinje inicijalizacijom k predstavnika pomoću jednostavne heuristike (kao što je slučajno uzorkovanje iz originalnih podataka), a zatim iterativno unapređuje predstavnike i dodelu klastera na sledeći način:
Korak dodele: Svakoj tački podataka dodeljuje se njen najbliži predstavnik iz skupa S koristeći funkciju rastojanja Dist(·, ·), a odgovarajući klasteri se označavaju sa C₁ … Cₖ.
Korak optimizacije: Određuje se optimalni predstavnik yⱼ za svaki klaster Cⱼ koji minimizuje njegovu lokalnu ciljnu funkciju \(∑_{x_𝑖 ∈ 𝐶_𝑗} Dist(x_i,y_𝑗)\)
Algoritmi zasnovani na predstavnicima
- Različita rastojanja i različiti načini određivanja predstavnika - različite varijacije šireg pristupa
- Ciljna funkcija poboljšava se kroz više iteracija
- Kada je poboljšanje ciljne funkcije u jednoj iteraciji manje od korisnički definisanog praga, algoritam se može zaustaviti
- Algoritam se obično završava posle malog konstantnog broja iteracija
- Glavno usko grlo ovog pristupa je korak dodele, u kojem je potrebno izračunati rastojanja između svih parova tačka–predstavnik
- Vremenska složenost svake iteracije je O(k · n · d)
Primer
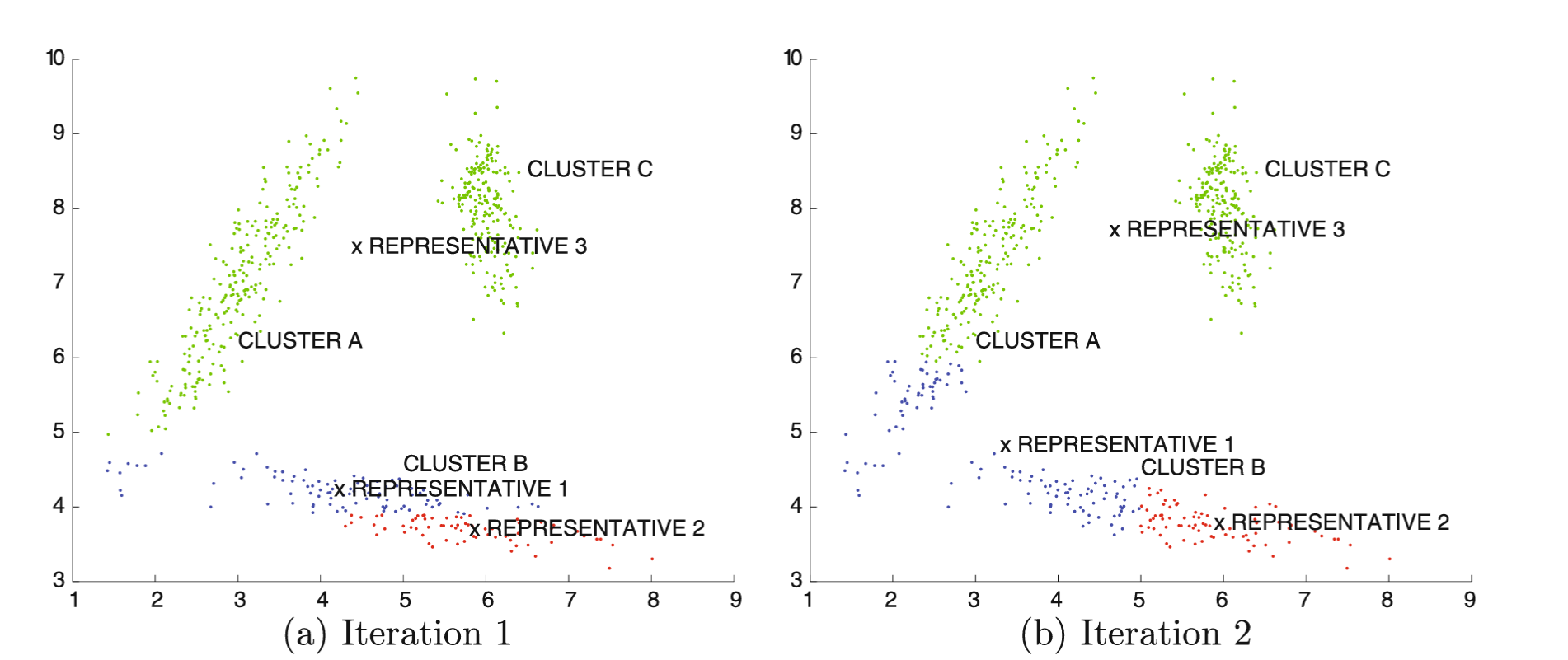
Primer
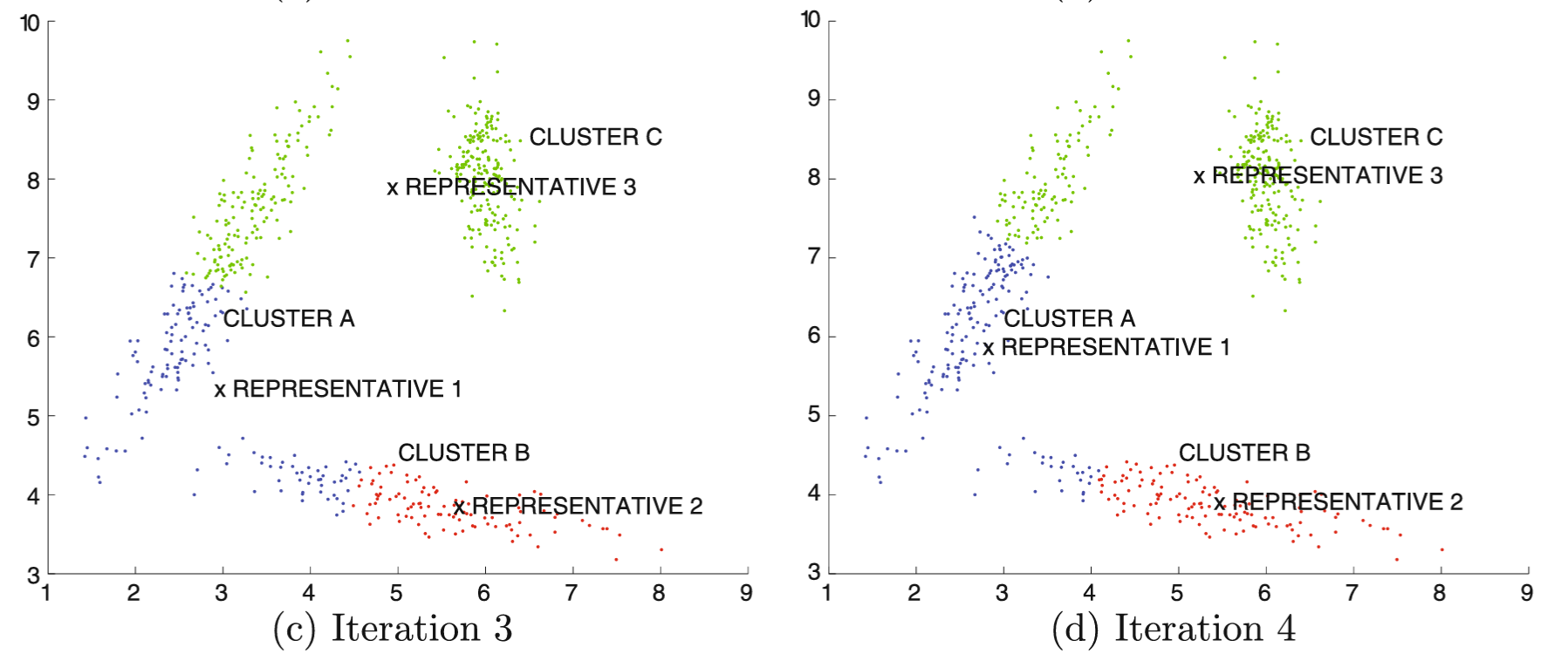
Primer
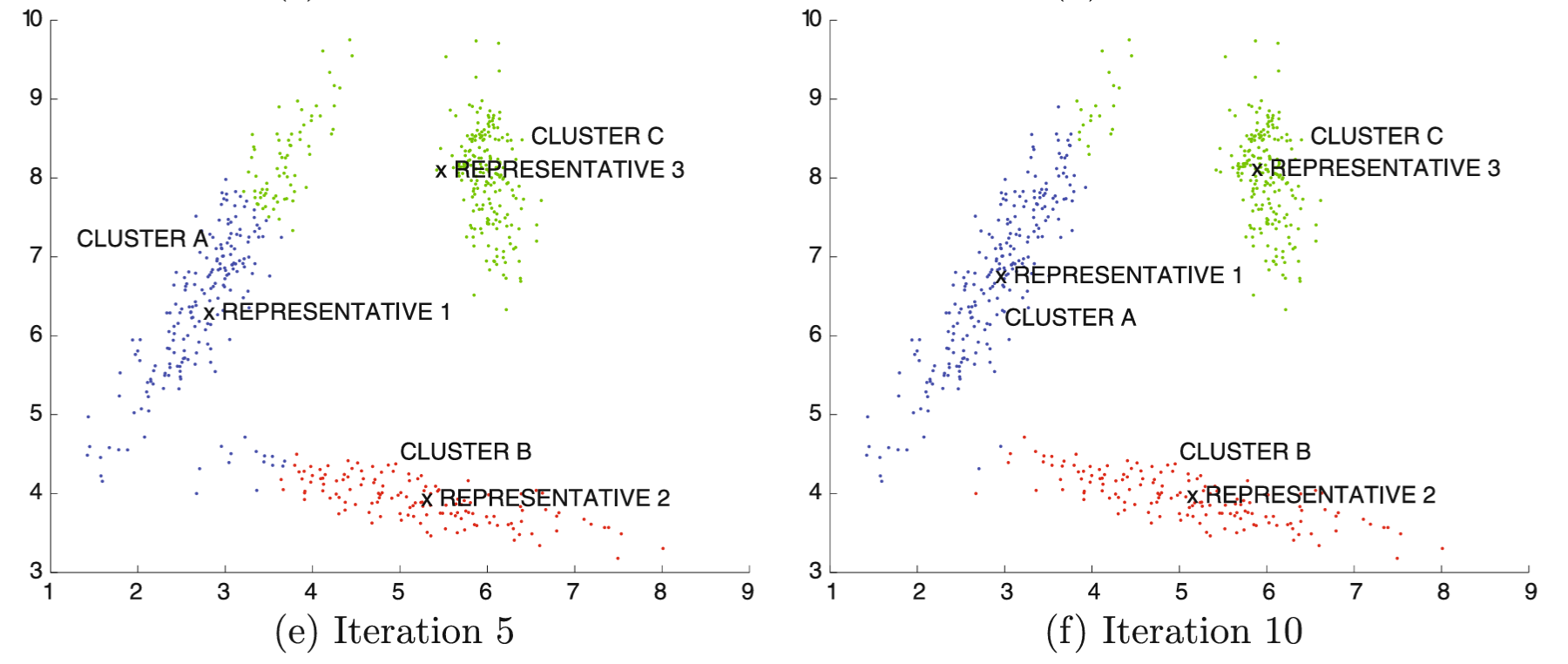
Algoritmi zasnovani na predstavnicima
- Varijacije okvira sa k predstavnika definisane su izborom funkcije rastojanja Dist(xᵢ, yⱼ) između tačaka podataka xᵢ i predstavnika xⱼ i tipom predstavnika klastera
Algoritam k-sredina
- Algoritam k-sredina (eng. k-means)
- Mera rastojanja - Euklidsko rastojanje
- Ciljna funkcija SSE (Sum of Squared Errors) minimizuje zbir kvadratnih grešaka nad svim tačkama podataka
- Predstavnik - srednja vrednost tačaka podataka u klasteru 𝐶𝑗
- Algoritam k-sredina ne daje dobre rezultate kada klasteri imaju proizvoljan oblik
Algoritam k-medijana
- Algoritam k-medijana (eng. k-medians)
- Kao funkcija rastojanja koristi se Manhattan rastojanje
- Predstavnik \(y_j\) je medijana tačaka podataka duž svake dimenzije u klasteru \(𝐶_𝑗\)
- Pošto se medijana bira nezavisno po svakoj dimenziji, dobijeni d-dimenzioni predstavnik ne mora pripadati originalnom skupu podataka 𝐷
- Algoritam k-medijana uopšteno bira predstavnike klastera na robustniji način nego k-sredina, jer je medijana manje osetljiva na izdvojene elemente van granica u klasteru u poređenju sa srednjom vrednošću
Algoritam k-medoida
- Algoritam k-medoida (eng. k-medoids)
- Predstavnici klastera se biraju iz baze podataka 𝐷
- Nekad je poželjno birati predstavnike iz skupa 𝐷 jer predstavnik klastera u algoritmu k-sredina može biti iskrivljen usled prisustva elemenata van granica u tom klasteru
- K-medoida se može definisati gotovo nad bilo kojim tipom podataka, pod uslovom da se nad tim tipom podataka može definisati odgovarajuća funkcija sličnosti ili rastojanja
Algoritam k-medoida
- Skup predstavnika 𝑆 se inicijalizuje kao skup tačaka iz originalne baze podataka 𝐷
- Skup 𝑆 se iterativno unapređuje zamenom jedne tačke iz skupa 𝑆 sa jednom tačkom iz baze podataka 𝐷
- Iterativna zamena može se posmatrati kao strategija penjanja uzbrdo, jer skup 𝑆 definiše jedno rešenje problema klasterovanja, a svaka zamena predstavlja jedan korak penjanja ka boljem rešenju.
- Da bi algoritam klasterovanja bio uspešan, svaka iteracija mora barem malo poboljšavati ciljnu funkciju problema
Algoritam k-medoida
- Postoji nekoliko mogućnosti za izvođenje zamene:
- isprobati sve kombinacija zamene jednog predstavnika iz skupa 𝑆 jednom tačkom iz skupa 𝐷, i zatim izabrati najbolju zamenu - izuzetno skupo
- nasumično izabran skup od 𝑟 parova \((x_𝑖,y_𝑗)\) za moguću zamenu. Najbolji par među ovih r kandidata koristi se za zamenu
- Algoritam k-medoida je sporiji od algoritma k-sredina, ali ima širu primenljivost na različite tipove podataka
Praktična i implementaciona pitanja
- Inicijalizacija predstavnika
- Najjednostavniji kriterijum inicijalizacije jeste da se tačke biraju nasumično iz prostora podataka, ili da se uzorkuje originalna baza podataka 𝐷
- Algoritam k-predstavnika pokazuje iznenađujuću robustnost na izbor inicijalizacije, iako je moguće da algoritam formira suboptimalne klastere.
Praktična i implementaciona pitanja
- Uticaj elemenata van granice
- Prisustvo elemenata van granice obično ima negativan uticaj na ove algoritme
- Algoritam k-medoida često eliminiše izdvojenog predstavnika tokom iterativne zamene
Praktična i implementaciona pitanja
- k-sredina pristup može ostati zaglavljen sa:
- klasterom koji sadrži samo jednu tačku
- praznim klasterom u narednim iteracijama
- U takvim slučajevima, jedno rešenje je da se u iterativni deo algoritma doda dodatni korak koji:
- odbacuje centre sa veoma malim klasterima i
- zamenjuje ih nasumično izabranim tačkama iz skupa podataka
Praktična i implementaciona pitanja
- Izbor broja klastera k
- Broj klastera 𝑘 je ulazni parametar ovih algoritama
- Broj prirodnih klastera u podacima često je teško automatski odrediti
- Pošto taj broj nije poznat unapred, ponekad je poželjno koristiti veću vrednost k od procene strvarnog broja klastera. Time se:
- neki klasteri dele na više predstavnika, ali
- smanjuje rizik od pogrešnog spajanja različitih klastera
- Kao korak naknadne obrade moguće je spojiti neke klastere na osnovu međuklasterskih rastojanja
Hijerarhijski algoritmi klasterovanja
- Ideja: formiranje skupa ugneždenih klastera koji su organizovani u obliku hijerarhije po nivoima
- Rezultati se obično prikazuju pomoću dendograma
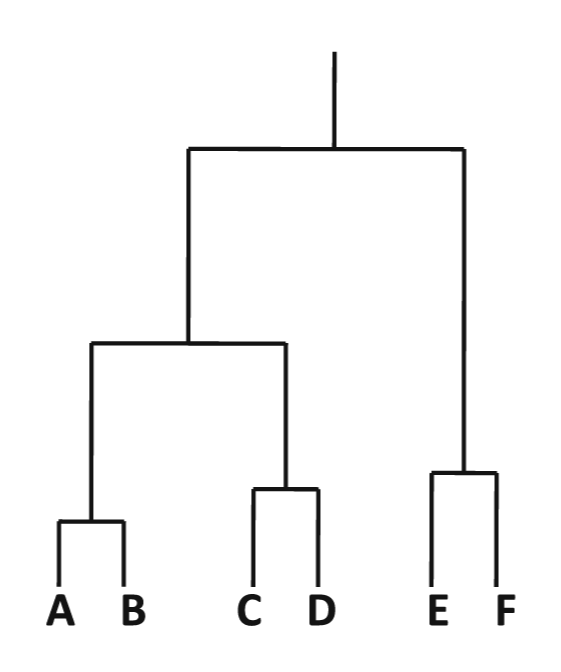
Hijerarhijski algoritmi klasterovanja
- Postoje dve osnovne vrste hijerarhijskih algoritama, u zavisnosti od načina izgradnje hijerarhijskog stabla klastera:
- Aglomerativni pristup - sakupljajuće klasterovanje
- Divizivni pristup - razdvajajuće klasterovanje
Hijerarhijski algoritmi klasterovanja
- Aglomerativni pristup - sakupljajuće klasterovanje
- Pojedinačne tačke podataka se postepeno spajaju u klastere višeg nivoa
- Glavna razlika između metoda je u izboru veze koja određuje koje klastere treba spojiti
Hijerarhijski algoritmi klasterovanja
- Divizivni pristup - razdvajajuće klasterovanje
- Podaci se sukcesivno dele u strukturu nalik stablu
- U pojedinim koracima može se koristiti algoritam ravnog klasterovanja za podelu klastera
- Primeri strategija rasta stabla:
- Deljenje najvećeg čvora → listovi sa sličnim brojem tačaka
- Izgradnja strogo balansiranog stabla, sa istim brojem potomaka u svakom čvoru → listovi sa različitim brojem tačaka
Aglomerativni pristup - sakupljajuće klasterovanje
- Tačke podataka se sukcesivno spajaju u klastere višeg nivoa
- Algoritam započinje sa pojedinačnim tačkama podataka, pri čemu je svaka tačka u svom zasebnom klasteru, i zatim ih postepeno spaja u klastere višeg nivoa.
- U svakoj iteraciji biraju se dva klastera za koja se smatra da su međusobno najbliža.
- Ovi klasteri se spajaju i zamenjuju novonastalim, spojenim klasterom
- Svaki korak spajanja smanjuje broj klastera za 1.
Aglomerativni pristup - sakupljajuće klasterovanje
- Potrebno je definisati metod za merenje bliskosti između klastera koji sadrže više tačaka podataka, kako bi se moglo odlučiti koje klastere treba spojiti
- Neka je n broj tačaka podataka u d-dimenzionoj bazi podataka 𝐷, a neka je \(𝑛_𝑡=𝑛−𝑡\) broj klastera nakon 𝑡 spajanja
- U svakom trenutku, održava se matrica rastojanja 𝑀 dimenzije \(𝑛_𝑡x𝑛_𝑡\) između trenutno postojećih klastera u podacima
Aglomerativni pristup - sakupljajuće klasterovanje
- U svakoj iteraciji algoritma bira se (nediagonalni) element u matrici rastojanja sa najmanjom vrednošću rastojanja, a odgovarajući klasteri se spajaju
- Dimenzionalnost matrice se u svakom koraku smanjuje za 1
- Potrebno je obrisati redove i kolone koji odgovaraju spojenim klasterima, i dodati novi red i kolonu rastojanja koji odgovaraju novonastalom klasteru
- Algoritam za određivanje vrednosti ovog novog reda i kolone zavisi od načina izračunavanja rastojanja između klastera u postupku spajanja
Aglomerativni pristup - sakupljajuće klasterovanje
- Kao kriterijum zaustavljanja, mogu se koristiti dve opcije:
- maksimalni prag nad rastojanjem između dva klastera koja se spajaju, ili
- minimalni prag nad brojem klastera
- Maksimalni prag ima za cilj da automatski odredi prirodan broj klastera u podacima, ali ima nedostatak jer zahteva specificiranje praga kvaliteta koji je teško intuitivno odabrati
- Minimalni prag ima prednost jer je intuitivno razumljiv u smislu željenog broja klastera u podacima
Veze između klastera
- Neka su indeksi dva klastera koja treba spojiti označeni sa 𝑖 i 𝑗
- Rastojanje između dve grupe objekata izračunava se kao funkcija svih \(𝑚_𝑖⋅𝑚_𝑗\) parova rastojanja između njihovih objekata.
- Načini izračunavanja rastojanja između dve grupe objekata su:
- Najbolja (jednostruka) veza – single linkage: rastojanje je jednako minimalnom rastojanju između svih \(𝑚_𝑖⋅𝑚_𝑗\) parova objekata.
- dobra za otkrivanje klastera proizvoljnog oblika
- može i pogrešno spojiti različite klastere ako je uzrokovano šumom u podacima.
Veze između klastera
- Potpuna veza – complete linkage: rastojanje između dve grupe objekata jednako je maksimalnom rastojanju između svih \(𝑚_𝑖⋅𝑚_𝑗\) parova objekata u te dve grupe.
- Kriterijum potpune veze pokušava da minimizuje maksimalni prečnik klastera, definisan kao najveće rastojanje između bilo kog para tačaka u klasteru
Veze između klastera
- Grupno-prosečna veza – average linkage: rastojanje između dve grupe objekata jednako je prosečnom rastojanju između svih \(𝑚_𝑖⋅𝑚_𝑗\) parova objekata u grupama
- Najbliži centroid – closest centroid: u svakoj iteraciji se spajaju klasteri čiji su centroidi najbliži.
- Nedostatak: centroidi gube informaciju o rasprostranjenosti različitih klastera.
- Npr. ovakav metod neće praviti razliku između spajanja klastera različitih veličina, sve dok su njihovi centroidi na istom rastojanju
Veze između klastera
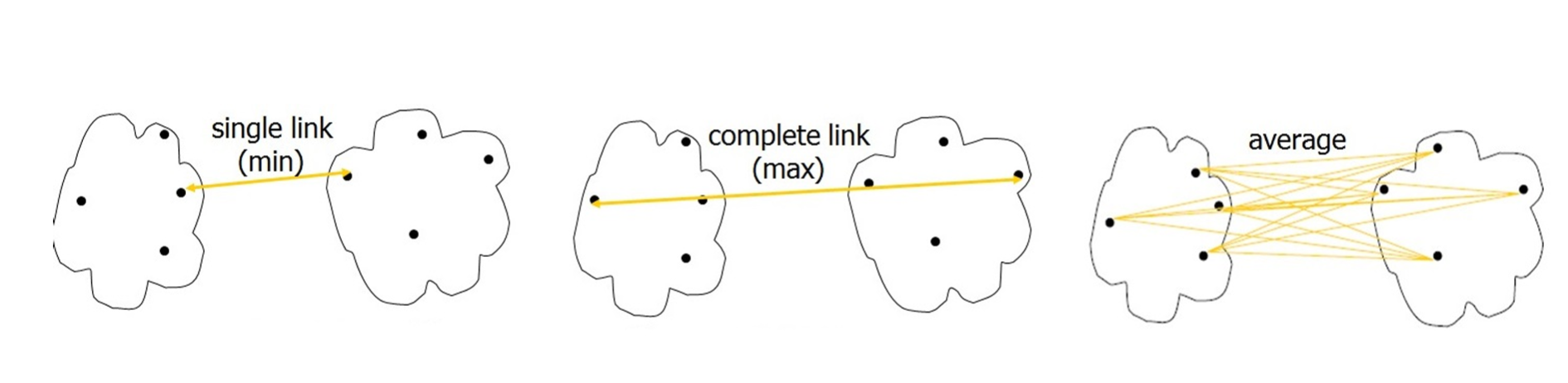
Veze između klastera
- Različiti kriterijumi imaju različite prednosti i nedostatke
- Metoda jednostruke veze može sukcesivno spajati lance blisko povezanih tačaka i tako otkrivati klastere proizvoljnog oblika. Međutim, isto svojstvo može dovesti i do neprikladnog spajanja nepovezanih klastera ako je ulančavanje posledica šuma u podacima.
Veze između klastera
- Metoda potpune (najgore) veze nastoji da minimizuje maksimalno rastojanje između bilo kog para tačaka u klasteru.
- Ova veza teži da minimizaciju prečnik klastera i da formira klastere sličnog prečnika.
- Ako su neki prirodni klasteri u podacima veći od drugih, ovaj pristup će razbiti veće klastere.
- Teži da formira klastere sfernog oblika, bez obzira na stvarnu raspodelu podataka.
- Problem metode potpune veze je i što daje preveliku važnost tačkama na šumovitim ivicama klastera, zbog fokusa na maksimalno rastojanje između bilo kog para tačaka u klasteru.
- Metode grupnog proseka otpornija je na šum, jer koristi više veza u izračunavanju rastojanja.
Praktična razmatranja
- Mana ovih metoda je osetljivost na mali broj grešaka napravljenih tokom procesa spajanja
- Npr. ako se u nekoj fazi donese pogrešna odluka o spajanju zbog prisustva šuma u skupu podataka, takva greška se ne može poništiti, već se može dalje propagirati kroz naredna spajanja
Razdvajajuće (divizivne) metode
- Razdvajajuće metode mogu se posmatrati kao meta-algoritmi opšte namene koji kao potproceduru koristite drugi algoritam klasterovanja
- Algoritam inicijalizuje stablo u korenom čvoru koji sadrži sve tačke podataka. U svakoj iteraciji, skup podataka u određenom čvoru trenutnog stabla deli se na više čvorova (klastera).
- Promenom kriterijuma za izbor čvora koji se deli, mogu se konstruisati stabla balansirana po visini ili stabla balansirana po broju klastera.
Razdvajajuće (divizivne) metode
RazdvajajućiAlgoritam(Podaci: D, Algoritam: A)
begin
Inicijalizuj stablo T sa korenim čvorom koji sadrži D;
repeat
Izaberi list L u stablu T na osnovu unapred
definisanog kriterijuma;
Primeni algoritam A da se čvor L podeli
na čvorove L1, …, Lk;
Dodaj čvorove L1, …, Lk kao decu čvora L u stablu T;
until kriterijum zaustavljanja je ispunjen;
endRazdvajajuće (divizivne) metode
- Algoritam rekurzivno deli čvorove pristupom odozgo na dole sve dok se ne dostigne određena visina stabla ili dok svaki čvor ne sadrži manje od unapred definisanog broja objekata.
Bisekcija k-sredina
- Bisekcija k-sredina je razdvajajući hijerarhijski algoritam u kome se svaki čvor deli na tačno dva potomka primenom 2-sredina algoritma
- Da bi se čvor podelio na dva potomka bira se ono deljenje koje ima najbolji uticaj na ukupnu ciljnu funkciju klasterovanja
- Postoji više varijanti ovog pristupa koje koriste različite strategije rasta stabla za izbor čvora koji će se sledeći deliti.
- Npr. može se prvo deliti najteži čvor ili čvor sa najmanjim rastojanjem od korena
Algoritmi zasnovani na mreži i gustini
- Osnovna ideja ove grupe algoritama je da se najpre identifikuju guste oblasti u podacima i da čine gradivne blokove za konstruisanje klastera proizvoljnog oblika - Ove oblasti se mogu posmatrati i kao pseudo-tačke podataka koje zatim treba pažljivo ponovo klasterovati u grupe proizvoljnog oblika
- Postoje brojne varijacije ovog opšteg principa, u zavisnosti od konkretnog tipa izabranih gradivnih blokova. - Npr. kod algoritama zasnovanih na mreži, fini klasteri su regioni u prostoru podataka nalik mreži.
Algoritmi zasnovani na mreži
- Podaci se diskretizuju na 𝑝 intervala koji su najčešće jednake širine
- Za skup podataka dimenzionalnosti 𝑑, ovo dovodi do ukupno \(𝑝^𝑑\) hiperkocki u prostoru podataka
- \(𝑝^𝑑\) hiperkocki su gradivni blokovi na kojima se zasniva algoritam
Primer
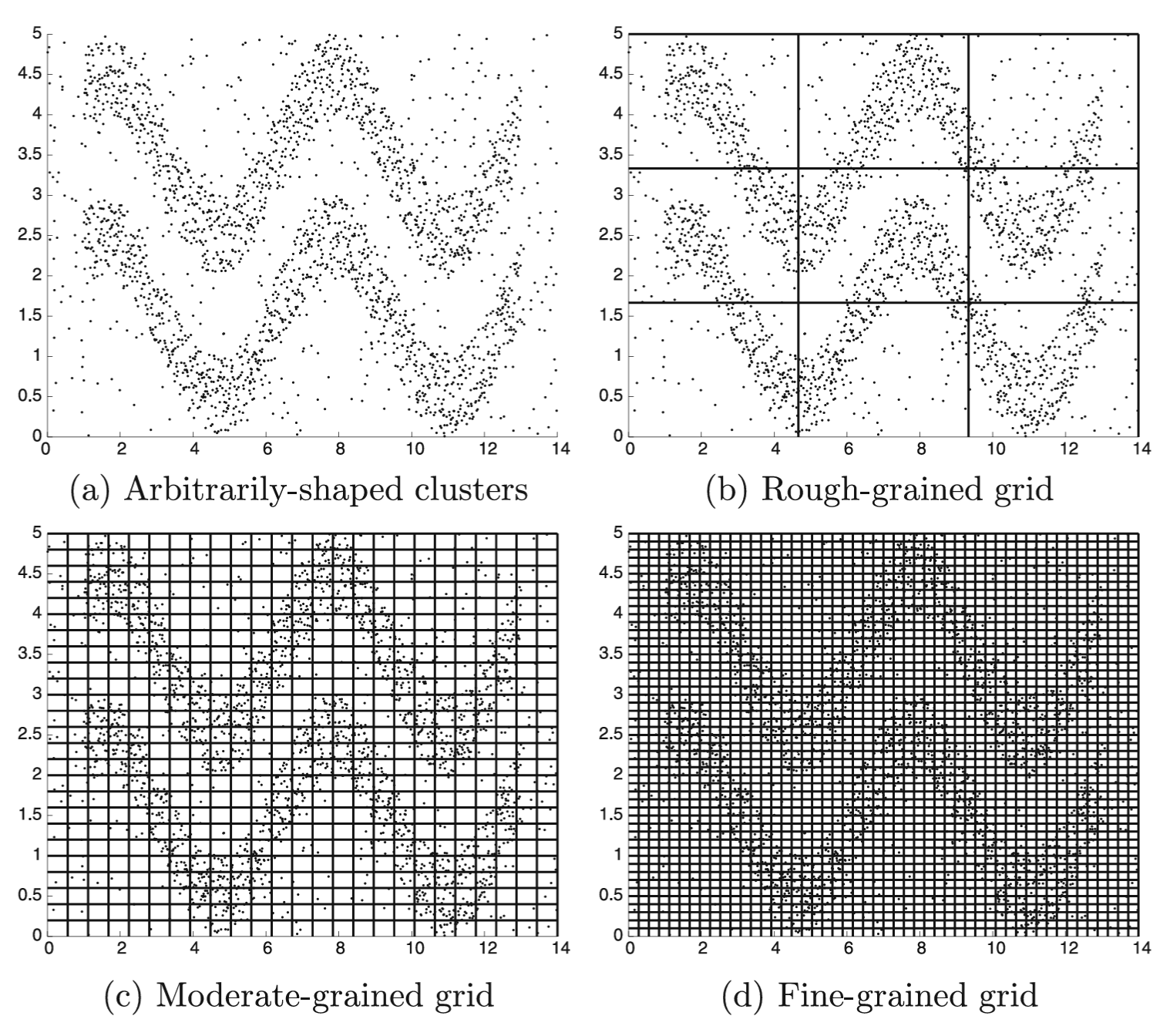
Algoritmi zasnovani na mreži
- Prag gustine 𝜏 koristi se za određivanje podskupa od \(𝑝^d\) hiperkocki koje se smatraju gustim.
- Dve mrežne oblasti su susedno povezane ako dele zajedničku stranicu (ili ugao u nekim definicijama)
- Uopštenje: dve mrežne oblasti su povezane po gustini ako se može pronaći put od jedne do druge koji se sastoji isključivo od niza susedno povezanih mrežnih oblasti.
- Cilj klasterovanja zasnovanog na mreži jeste da se odrede povezani regioni formirani od takvih ćelija mreže
Algoritmi zasnovani na mreži
- Takvi povezani regioni lako se određuju korišćenjem grafovskog modela nad mrežom
- Svaka gusta mrežna ćelija odgovara jednom čvoru u grafu, a svaka grana predstavlja susednu povezanost
- Tačke podataka koje pripadaju ovim povezanim komponentama predstavljaju klastere.
Algoritmi zasnovani na mreži
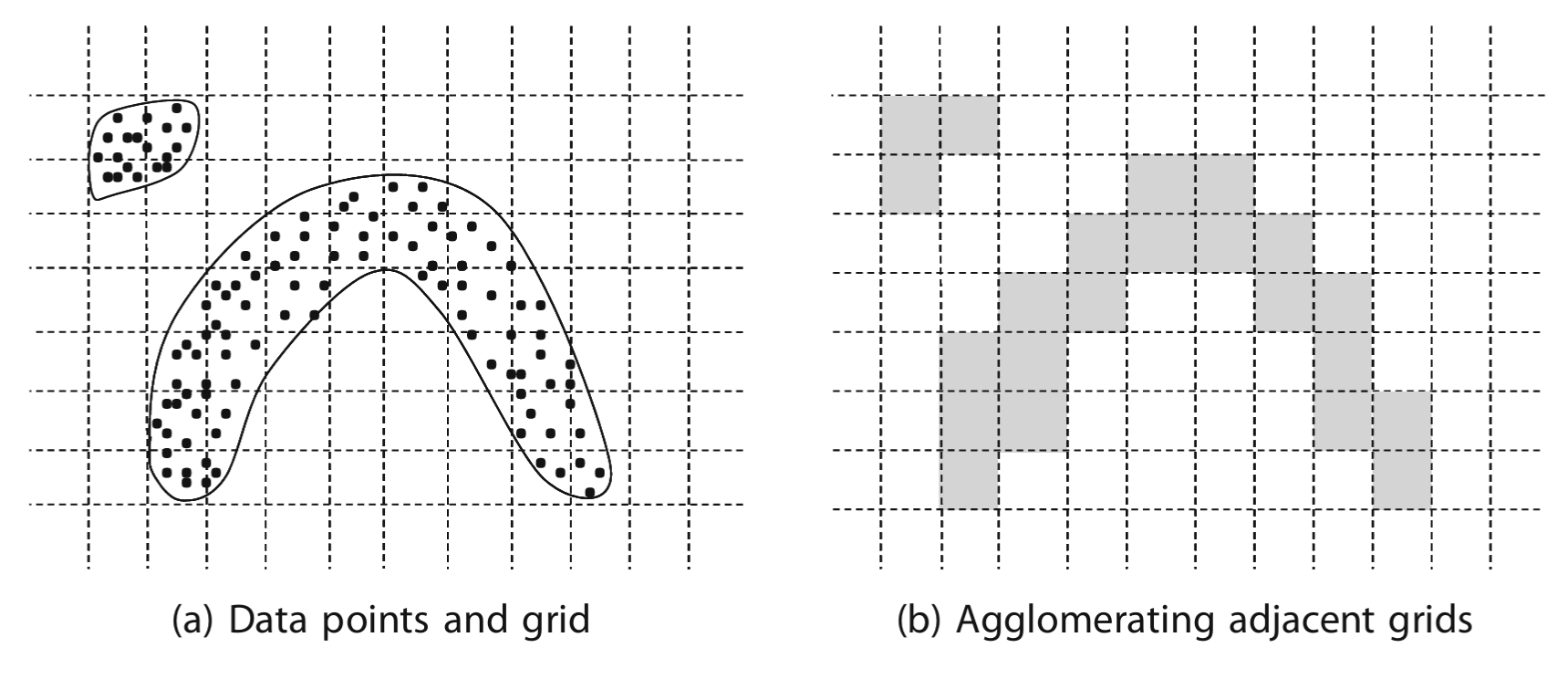
Algoritmi zasnovani na mreži
Algoritam GenerickaMreza(Podaci: D, Opsezi: p, Gustina: τ)
begin
Diskretizuj svaku dimenziju podataka D na p opsega;
Odredi guste ćelije mreže na nivou gustine τ;
Kreiraj graf u kome su guste ćelije povezane ako su susedne;
Odredi povezane komponente grafa;
return tačke u svakoj povezanoj komponenti kao klaster;
endAlgoritmi zasnovani na mreži
- Cilj algoritama je da se vrate prirodni klasteri u podacima, zajedno sa njihovim odgovarajućim oblicima, te se broj klastera ne zadaje unapred
- Potrebno je definisati dva parametra:
- broj intervala mreže 𝑝 i
- prag gustine 𝜏
Algoritmi zasnovani na mreži
- Pogrešan izbor parametra može dovesti do neželjenih posledica.
- Kada je broj intervala mreže previše mali, tačke podataka iz više klastera naći će se u istoj mrežnoj oblasti, što dovodi do neželjenog spajanja klastera.
- Kada je broj intervala mreže previše veliki, dolazi do velikog broja praznih mrežnih ćelija čak i unutar klastera. Kao posledica toga, prirodni klasteri u podacima mogu biti razdvojeni
Algoritmi zasnovani na mreži
- Kada je prag gustine 𝜏 suviše nizak, svi klasteri, uključujući i pozadinski šum, biće spojeni u jedan veliki klaster.
- Visok prag gustine može dovesti do toga da se neki klaster delimično ili u potpunosti propusti.
Praktični problemi
- Metode zasnovane na mreži ne zahtevaju unapred definisanje broja klastera i ne pretpostavljaju nikakav specifičan oblik klastera.
- Međutim, to se postiže po cenu potrebe da se definiše parametar gustine τ, koji sa analitičke tačke gledišta nije uvek intuitivan.
- Izbor rezolucije mreže takođe predstavlja izazov
- Jedan od glavnih izazova kod mnogih algoritama zasnovanih na gustini, uključujući i metode zasnovane na mreži, jeste to što koriste jedan globalni parametar gustine τ. Međutim, klasteri u stvarnim podacima mogu imati različite gustine.
Praktični problemi
- Ako je prag gustine izabran suviše visoko, klaster može biti propušten, a ako je prag gustine izabran suviše nisko, klasteri mogu biti veštački spojeni. U takvim situacijama, algoritmi zasnovani na rastojanju, kao što je k-means, mogu biti efikasniji od pristupa zasnovanog na gustini.
Praktični problemi
- Upotreba pravougaonih mrežnih regiona predstavlja aproksimaciju kod ove klase metoda. Ova aproksimacija postaje sve lošija sa porastom dimenzionalnosti, jer su pravougaoni regioni u prostorima velike dimenzionalnosti loša aproksimacija stvarnih klastera.
- Metode zasnovane na mreži postaju računarski neizvodljive u visoko-dimenzionalnim prostorima, jer broj mrežnih ćelija raste eksponencijalno sa porastom dimenzionalnosti podataka.
DBSCAN
- Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
- Kod algoritma DBSCAN se gustinske karakteristike pojedinačnih tačaka podataka koriste za njihovo spajanje u klastere.
- Pojedinačne tačke podataka u gustim regionima koriste se kao gradivni blokovi, nakon što se klasifikuju na osnovu svoje gustine.
- Gustina tačke podataka definiše se kao broj tačaka koje se nalaze unutar radijusa Eps oko te tačke (uključujući i samu tačku)
DBSCAN
- Gustine ovih sfernih regiona koriste se za klasifikaciju tačaka podataka: u jezgru (eng. core), granične (eng. border) i šum (eng. noise) tačke.
- Tačka podataka se definiše kao tačka u jezgru ako sadrži najmanje τ tačaka podataka unutar zadatog radijusa.
- Tačka podataka se definiše kao granična ako sadrži manje od τ tačaka u radijusu, ali se u radijusu Eps od nje nalazi se bar jedna tačka u jezgru.
- Tačka podataka koja nije ni u jezgru ni granična tačka definiše se kao šum tačka.
DBSCAN
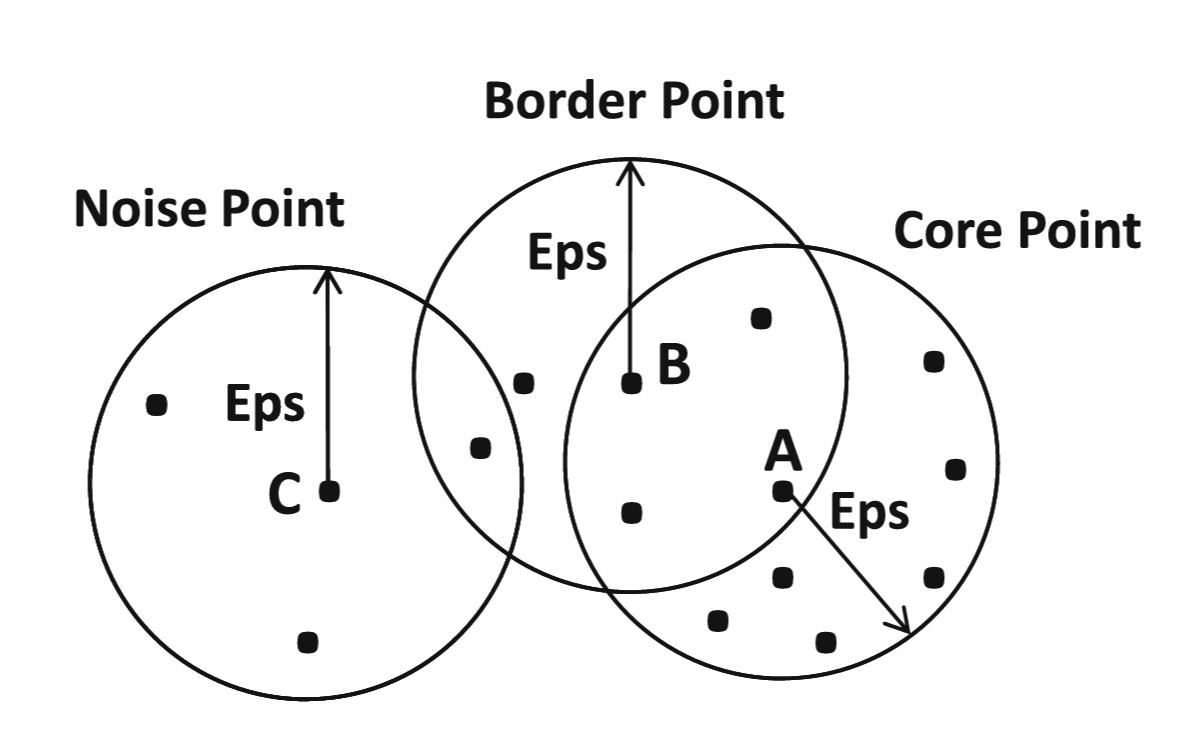
Primeri jezgrenih, graničnih i šumovitih tačaka za τ = 10.
DBSCAN
Algoritam DBSCAN(Podaci: D, Poluprečnik: Eps, Gustina: τ)
begin
Odredi u jezgru, granične i šum tačke skupa D
za (Eps, τ);
Napravi graf u kome su tačke *u jezgru* povezane
ako se nalaze na rastojanju manjem ili jednakom od Eps;
Odredi povezane komponente u grafu;
Dodeli svaku graničnu tačku onoj povezanoj komponenti sa kojom ima najjaču povezanost;
Vrati tačke u svakoj povezanoj komponenti kao klaster;
endDBSCAN
- Konstruiše se graf povezanosti u odnosu na tačke u jezgru, u kome svaki čvor odgovara jednoj tački u jezgru, a grana se dodaje između para tačaka u jezgru ako i samo ako se one nalaze na međusobnom rastojanju manjem ili jednakom Eps.
- Identifikuju se sve povezane komponente grafa koje predstavljaju klastere
- Granične tačke se dodeljuju onom klasteru sa kojim imaju najviši stepen povezanosti.
- Šum tačke se označavaju kao elementi van granica
Praktična pitanja
- DBSCAN pristup je veoma sličan metodama zasnovanim na mreži, osim što koristi kružne regione kao gradivne blokove.
- Upotreba kružnih regiona generalno obezbeđuje glatkije konture otkrivenih klastera.
- DBSCAN može da otkriva klastere proizvoljnog oblika i ne zahteva zadavanje broja klastera kao ulaznog parametra.
- DBSCAN je osetljiv na varijacije u lokalnoj gustini klastera.
DENCLUE
- DENCLUE (DENsity ClUstEring) je pristup klasterovanju zasnovan na gustini koji modeluje ukupnu gustinu skupa tačaka kao zbir funkcija uticaja pridruženih svakoj tački.
- Dobijena ukupna funkcija gustine ima lokalne maksimume gustine, i oni se mogu koristiti za prirodno definisanje klastera.
- Za svaku tačku podataka pronalazi se najbliži lokalni maksimum povezan sa tom tačkom, a skup svih tačaka podataka koje su povezane sa određenim lokalnim maksimumom gustine formira jedan klaster.
DENCLUE
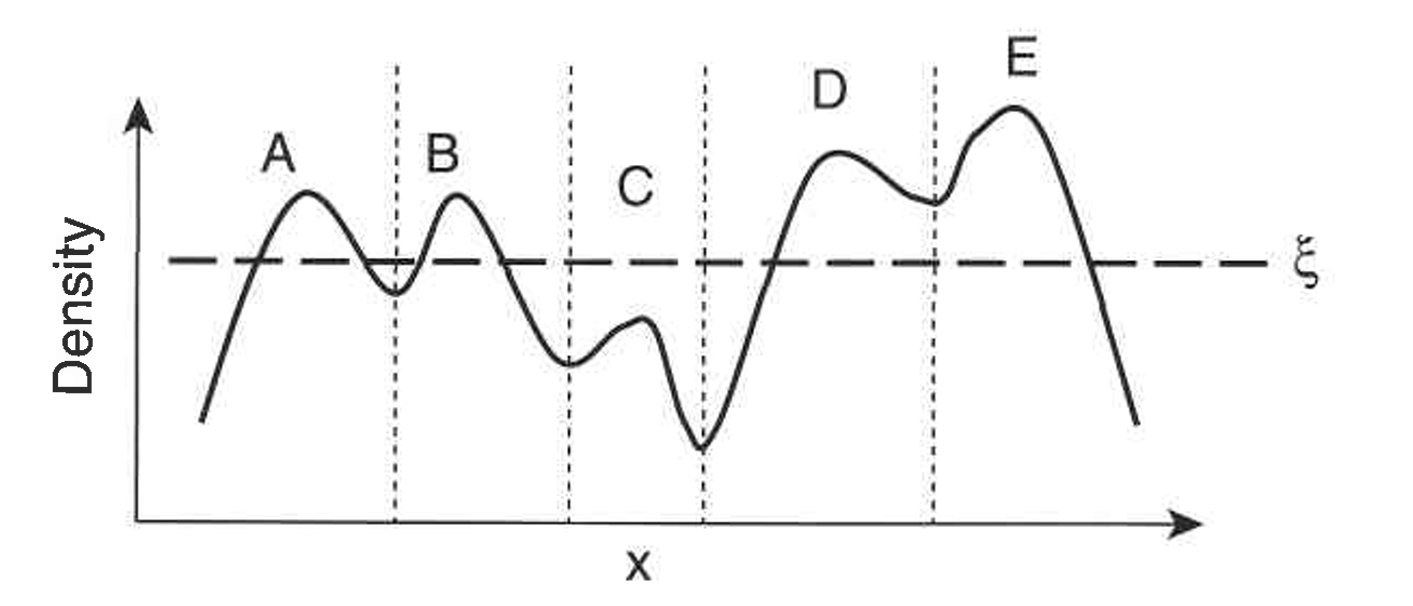
DENCLUE
- Ako je gustina u nekom lokalnom maksimumu suviše mala, tada se tačke u odgovarajućem klasteru klasifikuju kao šum i odbacuju.
- Ako se neki lokalni maksimum može povezati sa drugim lokalnim maksimumom putanjom tačaka podataka tako da je gustina u svakoj tački na toj putanji iznad minimalnog praga gustine, tada se klasteri povezani sa tim lokalnim maksimumima spajaju.
- Mogu se otkriti klasteri proizvoljnog oblika.
DENCLUE
DENCLUE algoritam
begin
Izvedi funkciju gustine za prostor koji zauzimaju tačke podataka;
Identifikuj tačke koje su lokalni maksimumi gustine;
Pridruži svaku tačku podataka odgovarajućem lokalnom maksimumu kretanjem u smeru
maksimalnog porasta gustine;
Definiši klastere koji se sastoje od tačaka pridruženih istom lokalnom maksimumu;
Odbaci klastere čiji lokalni maksimum ima gustinu manju od korisnički definisanog praga ε;
Spoji klastere koji su povezani putanjom tačaka čija je gustina jednaka ε ili veća;
endProcena gustine pomoću kernela
- DENCLUE se zasniva na dobro razvijenoj oblasti statistike i prepoznavanja obrazaca koja je poznata kao procena gustine pomoću kernela (eng. kernel density estimation).
- Cilj ovog skupa tehnika jeste da se raspodela podataka opiše pomoću funkcije.
- Kod kernel-procene gustine, doprinos svake tačke ukupnoj funkciji gustine izražava se pomoću funkcije uticaja, odnosno kernel funkcije.
- Ukupna funkcija gustine predstavlja jednostavno zbir funkcija uticaja pridruženih svakoj tački.
- Vrednost (doprinos) funkcije uticaja ili kernel funkcije opada sa porastom rastojanja od posmatrane tačke.
Procena gustine pomoću kernela
- Na primer, za neku konkretnu tačku 𝑥, često se kao kernel funkcija koristi Gausova funkcija: \[𝐾(y)=𝑒^{−\frac{distance(𝑥,y)^2}{2𝜎^2}} \] gde je
- σ parametar koji je analogan standardnoj devijaciji i koji određuje koliko brzo opada uticaj tačke sa povećanjem rastojanja.
Procena gustine pomoću kernela

Prednosti i ograničenja algoritma DENCLUE
- DENCLUE se dobro nosi sa šumom i elementima van granice
- Može da otkriva klastere različitih oblika i veličina
- Ima poteškoća sa visokodimenzionalnim podacima i sa skupovima podataka koji sadrže klastere znatno različitih gustina
Procena klasterovanja
- U mogim slučajevima kriterijum za validaciju kvaliteta algoritma su ciljne funkcije koju optimizuje određeni model klasterovanja
- Suma kvadrata greske (SSE- sum of the squared error)
- Kada se kao mera bliskosti koristi rastojanje u Euklidskom prostoru, za evaluaciju klasterovanja algortimom K-sredina često se koristi mera suma kvadrata greske (SSE)
Procena klasterovanja
\[SSE=\sum_{i=1}^K\sum_{x\in C_i} dist(c_i,x)^2\] gde je
x instanca skupa
\(C_i\) klaster
\(c_i\) centroid klastera \(C_i\)
Cilj je da SSE bude što manja.
Problem ovih kriterijuma nastaje prilikom poređenja algoritama sa različitim metodologijama
Procena klasterovanja
- Odnos intraklasterskog i interklasterskog rastojanja, Intra/Inter
- Uzorkuje se r parova instanci iz osnovnog skupa podataka
- P je skup parova koji pripadaju istom klasteru, prema klasterovanju koje je pronašao algoritam. Preostali parovi pripadaju skupu Q
Procena klasterovanja
- Prosečna intraklasterska i interklasterska rastojanja definišu se kao: \[Intra=\frac{\sum_{(𝑋_𝑖,𝑋_𝑗)∈𝑃}dist(𝑋_𝑖,𝑋_𝑗)}{∣𝑃∣}\]
\[Inter=\frac{\sum_{(𝑋_𝑖,𝑋_𝑗)∈Q}dist(𝑋_𝑖,𝑋_𝑗)}{∣Q∣}\]
- Male vrednosti ukazuju na bolje ponašanje klasterovanja
Procena klasterovanja
- Silueta koeficijent, eng. Silhouette coefficient
- Silueta koeficijent je mera koliko su instance grupisane sa instancama koje su slične njima samima.
- Prvo se silueta koeficijent računa za svaku instancu po formuli \[s =\frac{b-a}{max(a,b)}\] gde je
- a - prosečno rastojanje između instance i ostalih instanci u istom klasteru
- b - prosečno rastojanje između instance i svih instanci iz najbližeg susednog klastera
Procena klasterovanja
- Silueta koeficijent za ceo skup je prosečna vrednost koeficijenta za pojedinačne instance
- Vrednost silueta koeficijent je između [-1,1] pri čemu je
- -1 za neispravno grupisanje
- +1 za gusto grupisanje
- Vrednost koeficijent je veća kada su klasteri gusti i dobro razdvojeni
Procena klasterovanja
- Mere su dobre za poređenje klasterovanja dobijenih sličnom klasom algoritama ili različitih pokretanja istog algoritma
- Podešavanje parametara može se obaviti pomoću mera za procenu klasterovanja
- Ideja je da varijacija mere validacije može pokazati tačku prevoja ili tzv. lakat (eng. elbow) pri ispravnom izboru parametra
- Npr. kod k-sredina klasterovanja može se koristiti za podešavanje broja klastera k
- SSE mera će se smanjivati sa povećanjem broja klastera, ali će se smanjivati znatno sporije nakon tačke prevoja
- Mera kao što je odnos intraklasterskog i interklasterskog rastojanja će se smanjivati do tačke prevoja, a zatim može blago porasti
Procena klasterovanja
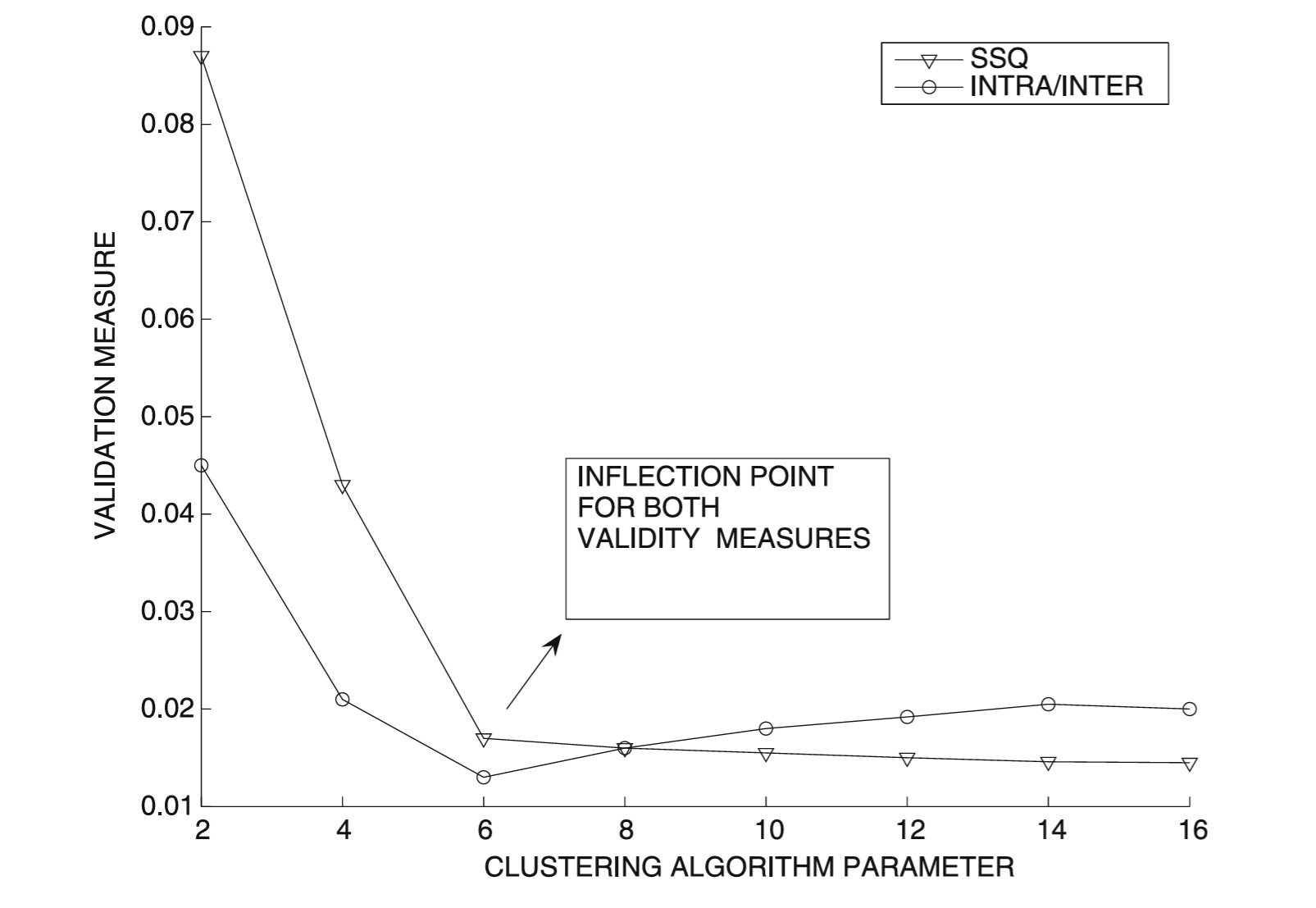
Klasterovanje - izazovi
- Izazovi kod klasterovanja:
- tip osnovnih podataka, npr. kategorički
- diskretne podatke je teško klasterovati
- zbog izazova u računanju bliskosti
- definisanja „centralnog” predstavnika klastera iz skupa kategoričkih tačaka podataka
- diskretne podatke je teško klasterovati
- tip osnovnih podataka, npr. kategorički
Klasterovanje - izazovi
- Izazovi kod klasterovanja:
- visoka dimenzionalnost
- veliki broj irelevantnih dimenzija
- masivni skupovi podataka
- neki algoritmi zahtevaju višestruke prolaze kroz podatke
- visoka dimenzionalnost
Klasterovanje - izazovi
- Izazovi kod klasterovanja:
- ocena kvaliteta dobijenih klastera
- postojanje alternativnih klasterovanja i može biti teško proceniti njihov kvalitet
- kada podaci sadrže šum, kvalitet klastera takođe može biti loš
- ocena kvaliteta dobijenih klastera
Klasterovanje kategoričkih podataka
- Problem klasterovanja kategoričkih (ili diskretnih) podataka predstavlja izazov jer su većina osnovnih operacija u klasterovanju podataka osmišljene za numeričke podatke
- Kategorički podaci mogu se transformisati u binarne podatke primenom procesa binarizacije
Klasterovanje kategoričkih podataka
- Algoritmi zasnovani na predstavnicima zahtevaju ponovljeno određivanje predstavnika (centroida) klastera, kao i određivanje sličnosti između predstavnika i instanci podataka
- Na višem nivou apstrakcije, ovi koraci ostaju isti i za kategoričke podatke
Klasterovanje kategoričkih podataka
- Centroid skupa kategoričkih podataka:
- Kod kategoričkih podataka centroid predstavlja histogram verovatnoća vrednosti za svaki atribut
- Za svaki atribut \(v_i\) i svaku moguću vrednost \(v_{ij}\), vrednost histograma \(p_{ij}\) predstavlja udeo instanci u klasteru za koje atribut \(i\) ima vrednost \(v_{ij}\)
- Za skup podataka dimenzionalnosti \(d\), centroid klastera predstavlja skup od \(d\) različitih histograma koji opisuju raspodelu verovatnoća kategoričkih vrednosti svakog atributa u klasteru
Primer histograma
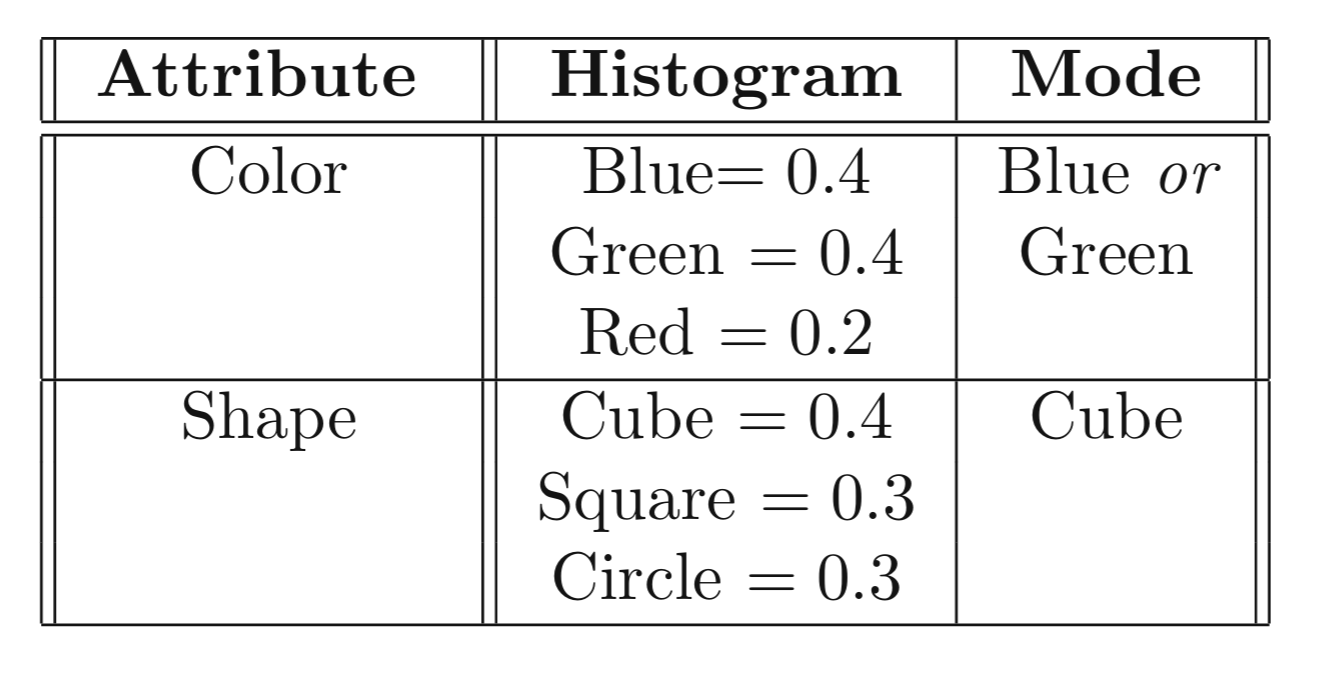
Klasterovanje kategoričkih podataka
- Izračunavanje sličnosti u odnosu na centroide:
- Najjednostavnija je sličnost zasnovana na poklapanju (eng. match-based similarity)
- Cilj je odrediti sličnost između histograma verovatnoća koji odgovara predstavniku i vrednosti kategoričkog atributa
- Ako atribut \(i\) ima vrednost \(v_{ij}\) za određenu instancu, tada je sličnost zasnovana na poklapanju \(p_{ij}\)
- Verovatnoće se sabiraju za sve atributa da bi se odredila ukupna sličnost
- Instanca se dodeljuje centroidu sa kojim ima najveću sličnost
- Ostali koraci k-sredina algoritma ostaju isti
k-modalno klasterovanje
- Svaka vrednost atributa za predstavnika bira se kao mod kategoričkih vrednosti tog atributa u klasteru
- Mod skupa kategoričkih vrednosti je vrednost koja ima najveću učestalost u skupu
- Mod je kategorička vrednosti \(v_j\) za svaki atribut \(i\) za koju histogram učestalosti ima najveću vrednost \(p_{ij}\)
- Prednosti pristupa zasnovanog na modu je što je predstavnik takođe kategorički zapis podataka, a ne histogram, te je lakše koristiti sličnosti za izračunavanje rastojanja između instanci i modova
Primer

k-modalno klasterovanje
- Na primer, funkcija sličnosti zasnovana na inverznoj učestalosti pojavljivanja (eng. inverse occurrence frequency)
\[S(x_i, y_i) = \begin{cases} \frac{1}{p_k(x_i)^2}, & \text{ako je } x_i = y_i \\ 0, \text{inače} \end{cases}\]
- gde je \(p_k(x)\) udeo instanci u kojima k-ti atribut u skupu podataka ima vrednost 𝑥
- Dobra za normalizaciju asimetrije u vrednostima atributa
Hijerarhijski algoritmi
- Sve dok se može definisati matrica rastojanja (ili sličnosti), većina algoritama može se primeniti i na podatke sa kategoričkim atributima
Hijerarhijski algoritam ROCK
- Algoritam ROCK (RObust Clustering using linKs) zasniva se na aglomerativnom pristupu odozdo nagore
- Klasteri se spajaju na osnovu kriterijuma sličnosti
- ROCK algoritam koristi kriterijum koji je zasnovan na meri zajedničkih najbližih suseda
- Pošto su aglomerativne metode relativno skupe u pogledu računanja, ROCK primenjuje ovaj pristup samo na uzorak tačaka podataka kako bi otkrio prototipske klastere
- Preostale tačke podataka se u završnom prolazu dodeljuju jednom od ovih prototipskih klastera
Hijerarhijski algoritam ROCK
- Prvi korak ROCK algoritma je transformacija kategoričkih podataka u binarnu reprezentaciju korišćenjem pristupa binarizacije
- Svaki objekat može se tretirati kao binarna transakcija, odnosno kao skup stavki
- Sličnost između dve transakcije računa se korišćenjem Žakardovog koeficijenta između odgovarajućih skupova: \[Sim(𝑇_𝑖,𝑇_𝑗)=\frac{∣𝑇_𝑖 ∩ 𝑇_𝑗∣}{∣𝑇_𝑖 ∪ 𝑇_𝑗∣}\]
- Dve instance \(𝑇_i\) i \(T_j\) definišu se kao susedi ako je sličnost \(Sim(𝑇_𝑖,𝑇_𝑗)\) veća od praga 𝜃
Hijerarhijski algoritam ROCK
- \(Link(T_i,T_j)\) označava funkciju sličnosti zasnovanu na zajedničkim najbližim susedima, koja je jednaka broju zajedničkih najbližih suseda između \(T_i\) i \(T_j\)
- Funkcija sličnosti \(Link(T_i,T_j)\) obezbeđuje kriterijum spajanja za aglomerativne algoritme
- Algoritam započinje tako što se svaka tačka podataka (iz inicijalno izabranog uzorka) nalazi u sopstvenom klasteru, a zatim se klasteri hijerarhijski spajaju na osnovu kriterijuma sličnosti između klastera
Hijerarhijski algoritam ROCK
- Sličnost između klastera se računa kao:
\[GroupLink(C_i,C_j)= \sum_{T_u∈C_i,T_v∈C_j} Link(T_u,T_v)\]
- Potrebno je normalizovati prema očekivanom broju međusobnih veza između para klastera, kako bi se osiguralo da spajanje većih klastera ne bude neopravdano favorizovano
Hijerarhijski algoritam ROCK
- Spajanja se izvode dok u podacima ne ostane ukupno k klastera
- Preostale tačke podataka dodeljuju se jednom od klastera
- Svaka tačka podataka dodeljuje se klasteru sa kojim ima najveću sličnost
Skalabilno klasterovanje podataka
- Kada je veličina skupa podataka veoma velika podaci se ne mogu čuvati u glavnoj memoriji, već moraju biti smešteni na disku
- Neki skalabilni algoritmi klasterovanja:
- CLARANS
- BIRCH
- CURE
Skalabilno klasterovanje podataka
- CLARANS predstavlja skalabilnu implementaciju algoritma k-medoid
- Algoritam BIRCH je hijerarhijska generalizacija algoritma k-sredina tipa odozgo nadole
- Algoritam CURE predstavlja aglomerativni pristup klasterovanju tipa odozdo nagore
CLARA
- Metode CLARA i CLARANS predstavljaju dve generalizacije pristupa k-medoid
- Metod Clustering LARge Applications (CLARA) zasniva se na posebnoj instanci k-medoida metode poznatoj kao particionisanje oko medoida (eng. partitioning around medoids, PAM).
CLARA
- U PAM, prilikom zamene jednog medoida sa drugim nemedoidnim predstavnikom, isprobavaju se svi mogući parovi od ukupno k⋅(n−k) kombinacija kako bi se poboljšala ciljna funkcija klasterovanja
- Od svih ovih parova bira se ona zamena koja daje najveće poboljšanje
- Proces zamene se ponavlja sve dok algoritam ne konvergira ka lokalno optimalnoj vrednosti
- Složenost se može smanjiti primenom algoritma na manji uzorak, tj. primenjuje se PAM na manji uzorkovani skup podataka veličine \(f⋅n\) kako bi se otkrili medoidi
- \(f\) je udeo uzorkovanja i vrednost je znatno manja od 1
CLARA
- Preostale tačke podataka dodeljuju se optimalnim medoidama koji su otkriveni primenom PAM-a na manjem uzorku
- Ovaj celokupni postupak se ponavlja više puta nad nezavisno izabranim uzorcima podataka iste veličine \(f⋅n\)
- Kao optimalno rešenje bira se ono klasterovanje koje daje najbolji rezultat među svim nezavisno izabranim uzorcima
- Glavni problem metode CLARA javlja se kada nijedan od unapred izabranih uzoraka ne sadrži dobre izbore medoida
CLARANS
- Pristup Clustering Large Applications based on RANdomized Search (CLARANS) radi sa celokupnim skupom podataka kako bi se izbegao problem unapred izabranih uzoraka
- Ovaj pristup iterativno pokušava zamene između nasumično izabranih medoida i nasumično izabranih nemedoida
- Nakon što se nasumično izabrani nemedoid pokuša zameniti sa nasumično izabranim medoidom, proverava se da li dolazi do poboljšanja kvaliteta klasterovanja. Ako se kvalitet poboljša, zamena se prihvata. U suprotnom, beleži se broj neuspešnih pokušaja zamene.
CLARANS
- Smatra se da je lokalno optimalno rešenje pronađeno kada se dostigne unapred zadat broj neuspešnih pokušaja, označen sa MaxAttempt.
- Ceo postupak pronalaženja lokalnog optimuma ponavlja se unapred definisan broj puta, označen sa MaxLocal
- Ciljna funkcija klasterovanja se zatim izračunava za svako od ovih MaxLocal lokalno optimalnih rešenja.
- Kao optimalno rešenje bira se ono koje je najbolje među ovim lokalnim optimumima.
- Prednost metode CLARANS u odnosu na CLARA jeste u tome što se istražuje znatno veća raznovrsnost prostora pretrage.
CLARANS
- Algoritam CLARANS
- može se generalizovati na različite tipove podataka
- nasleđuje relativno visoku računsku složenost metoda zasnovanih na k-medoid algoritmu
BIRCH
- Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH)
- Kombinacija hijerarhijskog klasterovanja tipa odozgo nadole i algoritma k-sredina.
- Koristi se hijerarhijska struktura podataka poznata kao CF-stablo (eng. CF-Tree)
- po visini balansirana struktura podataka koja hijerarhijski organizuje klastere
- svaki čvor ima faktor grananja najviše B, što odgovara njegovim B potklasterima, tj. deci
Primer CF-stablo
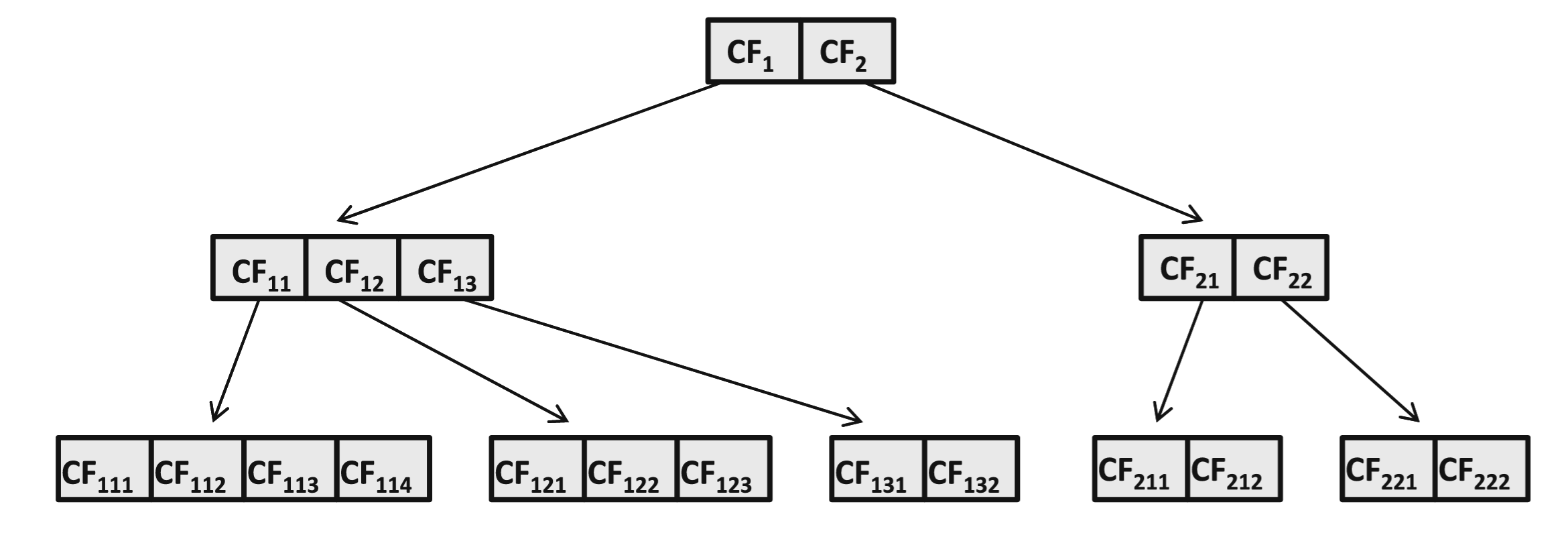
BIRCH
- Svaki čvor sadrži sažet prikaz svakog od najviše B potklastera na koje pokazuje
- Sažetak klastera naziva se klasterska karakteristika (eng. cluster feature, CF), odnosno vektor klasterskih karakteristika
- Sažetak sadrži trojku (SS, LS, m), gde je
- SS vektor koji sadrži zbir kvadrata tačaka u klasteru
- LS vektor koji sadrži linearni zbir tačaka u klasteru
- m broj tačaka u klasteru
- Veličina sažetka iznosi (2·d + 1) za skup podataka dimenzionalnosti d, i često se naziva CF-vektor
BIRCH
- Klasterska karakteristika ima dve osobine:
- Svaka klasterska karakteristika može se predstaviti kao zbir klasterskih karakteristika pojedinačnih tačaka podataka.
- Klasterska karakteristika roditeljskog čvora u CF-stablu jednaka je zbiru klasterskih karakteristika njegove dece
- Ažuriranje CF-vektora može se lako izvršiti dodavanjem CF-vektora nove instance CF-vektoru klastera
- Klasterska karakteristika roditeljskog čvora u CF-stablu jednaka je zbiru klasterskih karakteristika njegove dece
- Klasterske karakteristike mogu se koristiti za izračunavanje korisnih svojstava klastera - varijansu i centroid
BIRCH
- Centroid klastera je LS/m
- Varijanse duž i-te dimenzije mogu se izraziti kao \(\frac{𝑆𝑆_𝑖}{𝑚} −(\frac{𝐿𝑆_𝑖}{𝑚})^2\).
- \(SS_i\) i \(LS_i\) predstavljaju odgovarajuće komponente vektora za i-tu dimenziju
- Zbir ovih dimenziono-specifičnih varijansi daje varijansu celog klastera
- Rastojanje bilo koje tačke do centroida može se izračunati korišćenjem klasterske karakteristike, upotrebom već izračunatog centroida LS/m
- CF-vektor sadrži sve informacije potrebne za ubacivanje tačke podataka u CF-stablo
BIRCH
- Svaki list u CF-stablu ima prag varijanse T
- Vrednost T reguliše granularnost klasterovanja, visinu stabla i ukupan broj klastera u listovima
- Manje vrednosti T dovode do većeg broja finijih klastera
- Pošto se pretpostavlja da se CF-stablo nalazi u glavnoj memoriji, veličina skupa podataka ima presudan uticaj na izbor vrednosti T
BIRCH
- Manji skupovi podataka omogućavaju korišćenje manjeg praga T, dok veći skupovi zahtevaju veće vrednosti T
- Zbog toga inkrementalni pristup, kakav koristi BIRCH, postepeno povećava vrednost T kako bi se uravnotežila rastuća potreba za memorijom sa porastom veličine podataka
- Vrednost T mora se povećati kada CF-stablo više ne može da se zadrži u okviru raspoložive glavne memorije
BIRCH
- Inkrementalno dodavanje tačke podataka u stablo vrši se pristupom odozgo nadole.
- Na svakom nivou bira se najbliži centroid za dalje spuštanje kroz strukturu stabla
- CF-vektori se ažuriraju duž odgovarajuće putanje kroz stablo jednostavnim sabiranjem
- Na nivou lista, tačka podataka se dodaje u najbliži klaster samo ako to dodavanje ne poveća varijansu klastera iznad praga T. U suprotnom, mora se formirati novi klaster koji sadrži samo tu tačku podataka i ažurirati CF-stablo.
BIRCH
- Opciona faza poboljšanja klastera može se koristiti za grupisanje srodnih klastera unutar listova i uklanjanje malih izdvojenih (autlajer) klastera. Ovo se može postići korišćenjem aglomerativnog hijerarhijskog algoritma klasterovanja.
- Na kraju, opciona faza poboljšanja ponovo dodeljuje sve tačke podataka njihovim najbližim centrima, dobijenim u globalnoj fazi klasterovanja.
- Ova faza zahteva dodatno prolazak kroz podatke, a po potrebi se u njoj mogu ukloniti i autlajeri.
BIRCH
- Algoritam BIRCH je veoma brz, jer osnovni pristup (bez faze poboljšanja) zahteva jedan prolaz kroz podatke, a svako dodavanje predstavlja efikasnu operaciju.
- Mana je što nije projektovan za proizvoljne tipove podataka niti za klastere proizvoljnog oblika
CURE
- Clustering Using REpresentatives (CURE) predstavlja aglomerativni hijerarhijski algoritam koji koristi najbližu vezu
- Umesto izračunavanja rastojanja između svih parova tačaka u dva klastera tokom spajanja, algoritam koristi skup predstavnika kako bi se postigla veća efikasnost
CURE
- Predstavnici se pažljivo biraju tako da obuhvate oblik svakog od trenutnih klastera, čime se zadržava sposobnost otkrivanja klastere proizvoljnog oblika
- Prvi predstavnik bira se kao tačka podataka koja je najudaljenija od centra klastera, drugi predstavnik je ona tačka koja je najudaljenija od prvog, treći se bira kao tačka koja ima najveće rastojanje do najbližeg od prethodna dva predstavnika, i tako dalje.
- r-ti predstavnik je tačka podataka koja ima najveće rastojanje do najbližeg iz skupa postojećih (r − 1) predstavnika
CURE
- Predstavnici imaju tendenciju da se rasporede duž kontura klastera
- Uobičajeno se iz svakog klastera bira mali broj reprezentativa (na primer deset)
- Ovaj pristup zasnovan na najudaljenijim tačkama ima nepovoljnu osobinu da favorizuje izbor elemenata van granica
- Nakon što su predstavnici izabrani, oni se povlače (skupljaju) ka centru klastera kako bi se smanjio uticaj elemenata van granica
- Povlačenje se vrši zamenom predstavnika novom, sintetičkom tačkom podataka koja leži na duži L koja spaja predstavnika sa centrom klastera. Rastojanje između sintetičkog predstavnika i originalnog predstavnika jednako je delu \(𝛼∈(0,1)\) dužine duži 𝐿.
CURE
- Povlačenje je naročito korisno implementacijama aglomerativnog klasterovanja sa najbližom vezom zbog osetljivosti ovih metoda na predstavnike iz šuma na obodima klastera jer oni mogu dovesti do ulančavanja nepovezanih klastera
- CURE može da rukuje elementima van granica tako što periodično eliminiše male klastere tokom procesa spajanja. Ideja je da takvi klasteri ostaju mali zato što uglavnom sadrže autlajere.
CURE
- Radi dodatnog smanjenja složenosti, algoritam CURE izdvaja slučajni uzorak iz osnovnog skupa podataka i sprovodi klasterovanje nad tim uzorkom
- U završnoj fazi algoritma, sve tačke podataka dodeljuju se jednom od preostalih klastera tako što se bira klaster čiji je predstavnik najbliži toj tački
CURE
- Veće veličine uzorka mogu se efikasno koristiti pomoću tehnike particionisanja. U tom slučaju, uzorak se dalje deli na skup od p particija. Svaka particija se hijerarhijski klasteruje sve dok se ne dostigne željeni broj klastera ili dok se ne ispuni neki kriterijum kvaliteta spajanja.
- Ovi međuklasteri (iz svih particija) zatim se ponovo hijerarhijski klasteruju kako bi se dobio konačan skup od k klastera iz uzorkovanih podataka.
- Završna faza dodeljivanja primenjuje se na reprezentative dobijenih klastera.
- Algoritam CURE može da otkriva klastere proizvoljnog oblika
Klasterovanje podataka visoke dimenzionalnosti
- Podaci visoke dimenzionalnosti sadrže veliki broj irelevantnih atributa koje unose šum u proces klasterovanja
- Kada je veliki broj atributa irelevantan, podatke nije moguće razdvojiti u smislene klastere
- Rastojanja između svih parova tačaka podataka postaju veoma slična. Ovaj fenomen naziva se koncentracija rastojanja.
- Metode izbora atributa mogu smanjiti negativan uticaj irelevantnih atributa. Međutim, često nije moguće unapred ukloniti neki konkretan skup atributa, kada optimalan izbor atributa zavisi od lokalne strukture podataka.
Primer
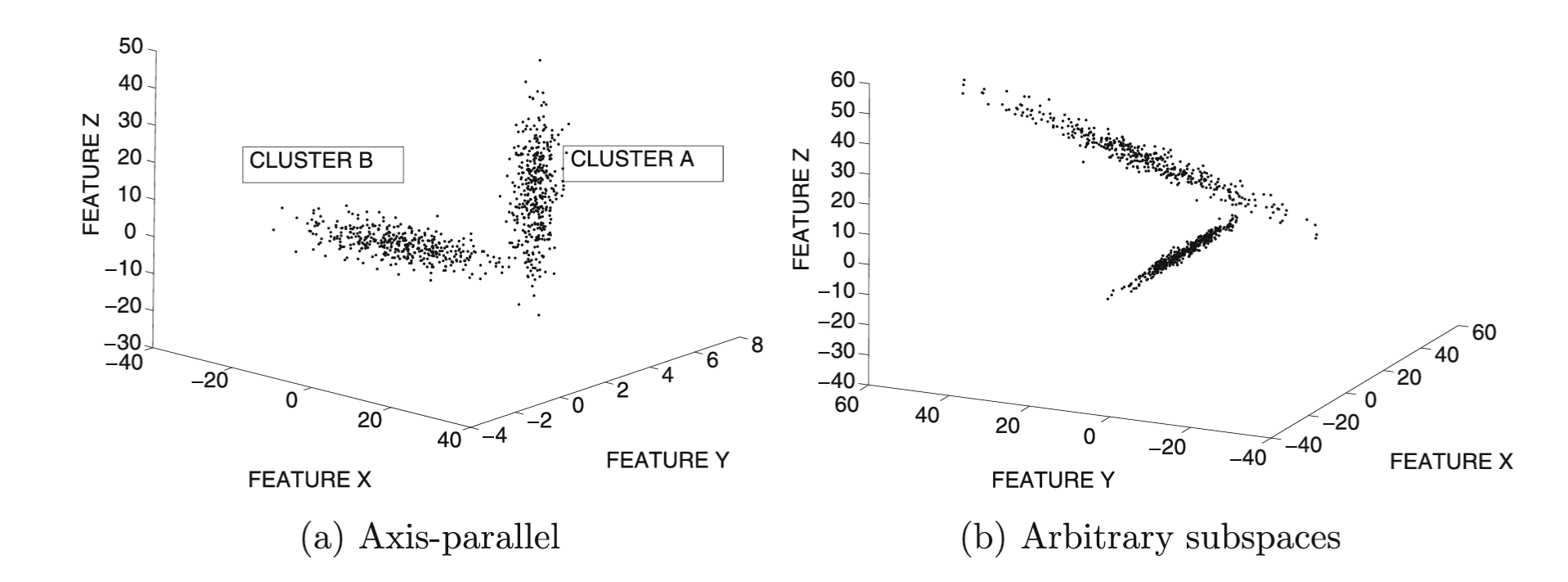
Klasterovanje podataka visoke dimenzionalnosti
- U konvencionalnim metodama klasterovanja, svaki klaster je skup tačaka.
Klasterovanje podataka visoke dimenzionalnosti
- Klasterovanje u potprostorima:
- Klasterovanje u potprostorima ima za cilj pronalaženje svih klastera u svim potprostorima celokupnog prostora obeležja
- Preklapanja između tačaka koje potiču iz različitih klastera su dozvoljena
- Ovaj problem je mnogo bliži otkrivanju obrazaca, gde se pravila pridruživanja pronalaze iz numeričkih podataka nakon diskretizacije
Klasterovanje podataka visoke dimenzionalnosti
- Svaki obrazac tada odgovara hiperkocki u okviru nekog potprostora numeričkih podataka, a tačke podataka unutar te hiperkocke predstavljaju klaster u potprostoru
- Broj otkrivenih klastera u potprostorima može biti veoma veliki, u zavisnosti od korisnički definisanog parametra, poznatog kao prag gustine.
Klasterovanje podataka visoke dimenzionalnosti
- Projektovano klasterovanje:
- U projektovanom klasterovanju, svaki klaster je definisan kao skup tačaka zajedno sa skupom dimenzija (odnosno potprostorom)
- Projektovani klaster definiše se kao par \((C_i,E_i)\), gde je \(C_i\) skup tačaka, a \(E_i\) potprostor definisan skupom atributa
- Preklapanja između tačaka koje potiču iz različitih klastera nisu dozvoljena
- Ova definicija pruža sažet opis podataka
Klasterovanje podataka visoke dimenzionalnosti
- CLIQUE predstavlja metodu klasterovanja u potprostorima.
- PROCLUS predstavljaju metodu projektovanog klasterovanja
CLIQUE
- CLustering In QUEst (CLIQUE) predstavlja generalizaciju metoda zasnovanih na mrežama
- Ulazni parametri metode su broj mrežnih intervala p za svaku dimenziju i gustina τ
- Gustina τ predstavlja minimalan broj tačaka podataka u gustoj mrežnoj ćeliji i može se posmatrati i kao minimalni zahtev podrške za mrežnu ćeliju
CLIQUE
- U prvoj fazi se koristi diskretizacija kako bi se formirala mrežna struktura
- Kod metoda zasnovanih na mrežama u punoj dimenzionalnosti, relevantne guste oblasti zasnivaju se na preseku diskretizacionih intervala preko svih dimenzija
- Glavna razlika između algoritma CLIQUE i ovih metoda jeste u tome što je cilj da se intervali odrede samo nad relevantnim podskupom dimenzija čija je gustina veća od τ
- Ovo je ekvivalentno problemu otkrivanja čestih obrazaca, gde se svaki diskretizovani interval tretira kao stavka, a prag podrške postavlja na τ
CLIQUE
- U originalnom CLIQUE algoritmu korišćen je metod Apriori, iako se u principu može koristiti bilo koji drugi metod za otkrivanje čestih obrazaca
- Kao i kod opštih metoda zasnovanih na mrežama, susedne mrežne ćelije (definisane nad istim potprostorom) se grupišu zajedno
- Ovaj postupak je identičan opštim metodama zasnovanim na mreži, osim što dve mrežne ćelije moraju biti definisane nad istim potprostorom da bi uopšte bile razmatrane kao susedne
- Svi pronađeni obrasci vraćaju se zajedno sa tačkama podataka koje im pripadaju
CLIQUE
- Za svaki skup povezanih mrežnih oblasti dimenzionalnosti k može se generisati i lako razumljiv opis, dekompozicijom tog skupa u minimalan skup k-dimenzionalnih hiperkocki
- Izlaz algoritma CLIQUE može biti veoma obiman i ponekad čak veći od veličine samog skupa podataka
PROCLUS
- PROCLUS (PROjected CLUStering)
- Klasterovanje za projektovano klasterovanje u visokodimenzionim podacima zasnovano na medoidima
- Svaki klaster ima sopstveni podprostor dimenzija koje su za njega relevantne
- Robustan na šum i irelevantne dimenzije
PROCLUS
- Algoritam ima tri faze:
- inicijalizacija
- bira mali skup kandidata M medoida
- iterativna optimizacija
- koristi tehniku klasterovanja zasnovanu na medoidima za postupno poboljšavanje rešenja sve do konvergencije
- unapređenje klastera
- dodeljuje instance skupa optimalnim medoidima i uklanja elemente van granica
- inicijalizacija
PROCLUS
Algoritam PROCLUS(Baza podataka: D, Broj klastera: k, Broj dimenzija: l)
begin
Izaberi kandidatski skup medoida M ⊆ D primenom pristupa najudaljenije tačke;
S = nasumično izabran podskup skupa M veličine k;
NajboljaVredCiljneFunkcije = ∞;
repeat
Izračunaj dimenzije (podprostor) pridružene svakom medoidu u skupu S;
Dodeli instance iz skupa D najbližim medoidima iz skupa S koristeći projektovanu udaljenost;
TrenVredCiljneFunkcije =
prosečna projektovana udaljenost instanci do centara njihovih klastera;
if (TrenVredCiljneFunkcije < NajboljaVredCiljneFunkcije)
Sbest = S;
NajboljaVredtCiljneFunkcije = TrenVredCiljneFunkcije;
end;
Ponovo izračunaj skup S zamenom loših medoida u skupu Sbest
nasumično izabranim tačkama iz skupa M;
until nije ispunjen kriterijum zaustavljanja;
Dodeli instance skupa medoidima iz skupa Sbest
koristeći unapređene podprostore;
vrati sve parove (klaster, podprostor);
endPROCLUS - faza inicijalizacije
- Mali skup kandidata za medoide M bira se tokom inicijalizacije:
- nasumično se bira uzorak M iz skupa podataka, čija je veličina proporcionalna broju klastera k, tj. A · k, gde je A>1
- primenom pohlepne metode smanjuje se veličina skupa M na B · k, gde važi A > B > 1
- primenjuje se pristup najudaljenije tačke, pri čemu se tačke iterativno biraju tako što se u svakom koraku bira instanca koja ima najveću udaljenost do najbliže od prethodno izabranih tačaka
PROCLUS - iterativna optimizacija
- Algoritam započinje izborom nasumičnog podskupa S od k medoida iz skupa M
- Postepeno poboljšava kvalitet medoida iterativnim zamenjivanjem loših medoida u trenutnom skupu novim tačkama iz skupa M
- Najbolji skup medoida čuva se u skupu Sbest
- Svaki medoid u skupu S povezan je sa skupom dimenzija koji predstavlja podprostor specifičan za odgovarajući klaster
- Skup dimenzija klastera se određuje na osnovu statističke raspodele instanci u lokalnoj okolini medoida
PROCLUS - iterativna optimizacija
- Algoritam određuje skup loših medoida u skupu Sbest
- Loši medoidi zamenjuju se nasumično izabranim tačkama iz skupa kandidata M, a zatim se meri uticaj te zamene na vrednost objektivne funkcije
- Ako se objektivna funkcija poboljša, tada se trenutni najbolji skup medoida Sbest ažurira na S.
- U suprotnom, u narednoj iteraciji se uzima druga nasumično izabrana zamena za loše medoide iz skupa Sbest.
- Ako se skup medoida Sbest ne poboljša tokom zadatog broja uzastopnih pokušaja zamene, algoritam se zaustavlja
- Sva izračunavanja, kao što su dodela tačaka i izračunavanje objektivne funkcije, izvršavaju se u podprostoru koji je pridružen svakom medoidu
PROCLUS - određivanje projektovanih dimenzija za medoid
- Za određivanje kvaliteta skupa medoida potrebno je dodeliti instance skupa medoidima
- Lokalnost medoida je skup instanci koje se nalaze unutar sfere čiji je poluprečnik jednak rastojanju do najbližeg drugog medoida
- Rastojanje instance do svakog medoida se računa u podprostoru \(E_i\) relevantnom za i-ti medoid
- Računa se (statistički normalizovano) prosečno rastojanje po svakoj dimenziji između medoida i instanci u njegovoj lokalnosti.
PROCLUS - određivanje projektovanih dimenzija za medoid
- Neka je \(r_ij\) prosečno rastojanje instanci u lokalnosti medoida i do tog medoida duž dimenzije j
- Računa se srednja vrednost \(𝜇_𝑖 = \sum_{𝑗=1}^𝑑 \frac{𝑟_{𝑖𝑗}}{d}\) i standardna devijacija \(𝜎_𝑖 = \sqrt \frac{\sum_{𝑗=1}^𝑑 (𝑟_{𝑖𝑗} − 𝜇_𝑖)^2}{𝑑−1}\) vrednosti rastojanja \(r_{ij}\), specifično za svaku lokalnost.
PROCLUS - određivanje projektovanih dimenzija za medoid
- Na osnovu toga dobija se statistički normalizovana vrednost \(z_{ij}\):
\[𝑧_{𝑖𝑗}=\frac{𝑟_{𝑖𝑗}−𝜇_𝑖}{𝜎_𝑖}\]
- Negativne vrednosti \(z_{ij}\) su posebno poželjne, jer ukazuju na manja prosečna rastojanja od očekivanih za dati par medoid–dimenzija
PROCLUS - određivanje projektovanih dimenzija za medoid
- Osnovna ideja je da se izaberu k · l najmanjih (najnegativnijih) vrednosti \(z_{ij}\) radi određivanja bitnih dimenzija specifičnuh za klastere.=
- Različiti klasteri mogu imati različit broj dimenzija
- Zbir ukupnog broja dimenzija pridruženih različitim medoidima mora biti jednak k · l
- Broj dimenzija pridruženih jednom medoidu mora biti najmanje 2
- Za svaki medoid se vrednosti \(z_{ij}\) sortiraju u rastućem redosledu i biraju se dve najmanje vrednosti. Zatim se preostalih k · (l − 2) parova medoid–dimenzija pohlepno bira kao najmanje vrednosti iz preostalih \(z_{ij}\).
PROCLUS - dodela instanci klasterima i evaluacija klastera
- Na osnovu medoida i njima pridruženih skupova dimenzija, instance se dodeljuju medoidima jednim prolazom kroz bazu podataka
- Rastojanje između instanci i medoida računa se pomoću segmentalne Menhetenove udaljenosti
- Segmentalna Menhetenova udaljenost je Menhetenova udaljenost normalizovana u odnosu na promenljiv broj dimenzija pridruženih svakom medoidu - računa se Menhetenova udaljenost koristeći samo relevantne dimenzije, a zatim se ta vrednost deli brojem relevantnih dimenzija
PROCLUS - dodela instanci klasterima i evaluacija klastera
- Instanca se dodeljuje medoidu sa kojim ima najmanju segmentalnu Menhetenovu udaljenost
- Objektivna funkcija klasterovanja se izračunava kao prosečna segmentalna Menhetenova udaljenost instanci do centara njihovih odgovarajućih klastera
- Ako se vrednost objektivne funkcije poboljša, tada se Sbest ažurira
PROCLUS - određivanje loših medoida
Određivanje loših medoida iz skupa Sbest vrši se na sledeći način
- Medoid klastera sa najmanjim brojem tačaka smatra se lošim
- Medoid svakog klastera koji ima manje od (n/k)⋅minDeviation instanci takođe se smatra lošim
- minDeviation je konstanta manja od 1, tipično 0,1
- Pretpostavka je da loši medoidi formiraju male klastere ili zato što su elementi van granica, ili zato što dele instance sa nekim drugim klasterom
- Loši medoidi se zamenjuju nasumično izabranim tačkama iz kandidatskog skupa medoida M
PROCLUS - faza unapređenja
- Završni prolaz kroz podatke vrši se kako bi se poboljšao kvalitet klasterovanja
- Dimenzije pridružene svakom medoidu računaju se drugačije nego u iterativnoj fazi
- Glavna razlika je u tome što se, prilikom analize dimenzija pridruženih svakom medoidu, koristi raspodela tačaka u klasterima dobijenim na kraju iterativne faze, umesto lokalnosti medoida.
PROCLUS - faza unapređenja
- Nakon računanja novih dimenzija, instance se ponovo dodeljuju medoidima na osnovu segmentalne Menhetenove udaljenosti u odnosu na novi skup dimenzija
- Elementi van granica se takođe obrađuju tokom ovog završnog prolaza kroz podatke
- Za svaki medoid i izračunava se njemu najbliži drugi medoid koristeći segmentalnu Menhetenovu udaljenost u relevantnom podprostoru medoida i Odgovarajuće rastojanje naziva se sfera uticaja tog medoida
- Ako je segmentalna Menhetenova udaljenost neke instance do svakog medoida veća od sfere uticaja tog medoida, tada se ta instanca odbacuje kao element van granica
Literatura
- Charu C. Aggarwal: Data Mining The Textbook, Springer, 2015.
- glave 6 i 7