Istraživanje podataka 2
2025/2026. šk. godina
Sadržaj kursa
- Istraživanje podataka - podsećanje (ili uvod)
- Priprema podataka
- Pravila pridruživanja
- Klasterovanje
- Klasifikacija
- Dodatne teme
- Istraživanje podataka i tekstualni podaci
- Istraživanje podataka i vremenske serije
- Istraživanje podataka i grafovski podaci
- …
Glavna literatura
- Charu C. Aggarwal: Data Mining The Textbook, Springer, 2015.
Obaveze
- Mogućnost polaganja ispita preko
- projekta: primena IP nad izabranim skupom podataka
- pregled oblasti/alata
Istraživanje podataka - definicije
proces sekundarne analize baza podataka sa ciljem pronalaženja neočekivanih odnosa koji su od interesa ili vrednosti za vlasnika baze podataka - Hand
proces izdvajanja tačnih, ranije nepoznatih, razumljivih i primenljivih informacija iz velikih baza podataka i njihove upotrebe za donošenje ključnih poslovnih odluka - Simoudis
Istraživanje podataka - definicije
- KDD (eng. Knowledge discovery in databases ) je proces korišćenja baze podataka, zajedno sa potrebnom selekcijom, preprocesiranjem, uzorkovanjem i transformacijama; zatim primene metoda (algoritama) istraživanja podataka radi izdvajanja obrazaca iz baze; kao i procene rezultata istraživanja podataka u cilju identifikovanja podskupa izdvojenih obrazaca koji se smatraju znanjem - Fayyad et al.
Istraživanje podataka - oblast
- ubrzan razvoj oblasti
- velika količina podataka je dostupna za probleme iz različitih oblasti
- Podaci su nova nafta – Clive Humby
- istraživanje (rudarenje) podataka (eng. data mining)
Glavne tehnike istraživanja podataka
- klasterovanje
- klasifikacija
- regresija
- pravila pridruživanja
- analiza elemenata van granica
Razumevanje istraživanja podataka
Pitanja na koja je potrebno odgovoriti pri planiranju istraživanja:
- Koji problem želite da rešite?
- Koji izvori podataka su dostupni i koji su delovi podataka bitni za trenutni problem?
- Koju vrstu preprocesiranja morate da uradite pre nego što počnete da koristite podatke?
- Koju tehniku/tehnike istraživanja podataka ćete koristiti? Kako ćete proceniti rezultate analize podataka?
- Kako ćete dobiti najveću korist od informacija koje ste dobili istraživanjem podataka?
Koraci u procesu istraživanja podataka
- razumevanje problema
- pronalaženje i/ili izdvajanje podataka koji mogu da se koriste za rešavanje problema
- analiza podataka
- priprema podataka za pravljenje modela
- pravljenje modela primenom tehnika istraživanja podataka
- evaluacija dobijenog modela
- primena modela
Dijagram procesa istraživanja podataka

CRISP-DM
CRISP-DM (Cross-Industry Standard Process for Data Mining) metodologija koja se pokazala uspešnom u industriji.
Faze:
- Razumevanje posla Utvrđivanje poslovnih ciljeva, određivanje ciljeva istraživanja podataka.
- Razumevanje podataka Podaci obezbeđuju sirovine za istraživanje podataka. Ova faza se bavi upoznavanjem izvora podataka i njihovih karakteristika. Uključuje prikupljanje početnih podataka, opisivanje podataka, upoznavanje podataka i proveru kvaliteta podataka.
CRISP-DM
Faze:
- Priprema podataka Odabir, čišćenje, konstruisanje, formatiranje podataka.
- Modeliranje Korišćenje metoda za analizu i dobijanje informacija iz podataka. Ova faza uključuje odabir tehnika, izgradnju i procenu modela.
- Evaluacija Procena rezultata i određivanje narednih koraka.
- Razvoj Integracija novih znanja u svakodnevne poslovne procese kako bi se rešio originalni poslovni problem.
Raznovrsni tipovi podataka
- istraživanje podataka predstavlja veliki izazov zbog velikih razlika u vrstama problema i tipovima podataka koji se javljaju u praksi
Raznovrsni tipovi podataka
Primeri:
pristupi korisnika veb dokumentima generišu logove na serverskoj strani i profile ponašanja korisnika na komercijalnim sajtovima
logovi pristupa korisnika mogu analizirati radi identifikovanja čestih obrazaca pristupa ili neuobičajenog ponašanja koje može ukazivati na zloupotrebu
povezana struktura veba - veb graf
veb dokumenti i njihova povezanost mogu se analizirati da bi se otkrile asocijacije između tema na internetu
Raznovrsni tipovi podataka
- Finansijske interakcije
- svakodnevne transakcije korišćenjem kartica
- transakcije se mogu koristit za otkrivanje prevara ili drugih neuobičajenih aktivnosti
Raznovrsni tipovi podataka
- interakcije korisnika
- korišćenje mobilnih telefona generiše zapis u telekomunikacionoj kompaniji
- analize takvih podataka otkrivaju obrasce ponašanja korisnika koji se koriste za donošenje odluka o kapacitetu mreže, promotivnim kampanjama, cenovnim modelima …
Podaci
- sirovi podaci često su nestrukturirani ili u formatu koji nije pogodan za automatsku obradu
- u praksi se najveći deo posla odnosi na pripremu podataka
- obrada podataka pre primene metoda istraživanja podataka
- prikupljanje
- čišćenje
- transformacija
- skladištenje u bazi podataka
Podaci
- najčešći oblik podataka je višedimenzioni, odnosno sastavljen od više atributa (promenljivih, polja, karakteristika) koji zajedno opisuju svaki objekat (slog, instanca, entitet, primer) u skupu podataka
Primer tabele
| Ime | Prezime | Indeks | Datum rođenja | Starost | Pol | Smer |
|---|---|---|---|---|---|---|
| Marko | Petrović | 2020/001 | 12.03.2000. | 25 | Muški | Računarstvo |
| Jelena | Jovanović | 2020/002 | 05.07.1999. | 26 | Ženski | Informacione tehnologije |
| Nemanja | Ilić | 2020/003 | 18.09.2001. | 24 | Muški | Softversko inženjerstvo |
| Sara | Radovanović | 2020/004 | 21.11.2000. | 25 | Ženski | Matematika |
| Ivan | Ristić | 2020/005 | 10.02.1998. | 27 | Muški | Računarstvo |
| Milica | Stojanović | 2020/006 | 04.06.2002. | 23 | Ženski | Statistika |
Tipovi atributa
- prema vrednosti
- kvantitativni
- starost u godinama
- kategorijski
- boja
- kvantitativni
Tipovi atributa
- prema broju vrednosti
- diskretni
- konačan broj
- etnička pripadnost, ime
- binarni atributi (npr. 1/0, da/ne, …)
- kontinuirani (neprekidni)
- temperatura, težina
- diskretni
Tipovi atributa prema operacijama
- diskretni
- imenski (\(=\), \(\neq\))
- naziv ulice, boja očiju, pol
- redni (\(=\), \(\neq\), \(<\), \(\leq\), \(>\), \(\geq\))
- ocena kvaliteta (loše, srednje, dobro, odlično), mesto na takmičenju (1,2,3)
- imenski (\(=\), \(\neq\))
Tipovi atributa prema operacijama
- neprekidni
- intervalni (\(=\), \(\neq\), \(<\), \(\leq\), \(>\), \(\geq\), \(+\), \(-\))
- ne postoji apsolutna nula koja predstavlja odsustvo nečega
- kalendarska godina, temperatura u stepenima Celzijusa
- razmerni (\(=\), \(\neq\), \(<\), \(\leq\), \(>\), \(\geq\), \(+\), \(-\), \(*\), \(/\))
- težina, dužina, cena
- intervalni (\(=\), \(\neq\), \(<\), \(\leq\), \(>\), \(\geq\), \(+\), \(-\))
Tipovi atributi
- asimetrični atributi - bitno je samo prisustvo ne-nula vrednosti
Primer asimetričnih atributa kod studenata Ime Prisustvovao predavanju Polagao ispit Prisutan na vežbama Dobio stipendiju Član studentske organizacije Marko 1 1 0 0 1 Jelena 1 1 0 1 0 Nemanja 0 0 1 0 0 Sara 0 0 1 0 0 Ivan 0 1 1 0 1 Milica 1 0 1 0 0 Petar 0 1 0 0 1 Teodora 1 1 1 0 0 Andrej 1 0 0 0 0 Marija 0 1 1 0 0
Tipovi podataka
- Tipovi podataka se mogu podeliti u dve grupe
- podaci bez zavisnosti
- podaci sa zavisnostima
Podaci bez zavisnosti
- jednostavni tipovi podataka
- ne postoje definisane zavisnosti između pojedinačnih objekata
- multidimenzionalni podaci
Podaci sa zavisnostima
različite vrednosti podataka mogu biti međusobno povezane vremenski, prostorno ili putem eksplicitnih mrežnih veza između pojedinačnih elemenata podataka
podaci sa zavisnostima se moraju posmatrati u okviru njihovih međusobnih odnosa i veza, što analizu čini složenijom i zahtevnijom
Podaci sa zavisnostima
Zavisnosti mogu biti:
- Implicitne zavisnosti
- uzastopne vrednosti temperature koje meri senzor verovatno će biti vrlo slične jedna drugoj
- Eksplicitne zavisnosti
- obično se odnosi na grafove gde se grane koriste za eksplicitno definisanje odnosa između elemenata
- društvene mreže - podaci o korisnicima predstavljaju čvorove, dok veze između njih predstavljaju grane koje su eksplicitne zavisnosti između podataka
Formati podataka
Formati podataka sa zavisnošću
- tekstualni
- prostorni
- vremenske serije
- grafovski
Tekst
- tekstualni podaci mogu se predstaviti kao
- niske
- multidimenzionalni podaci
- tekstualni dokument odgovara nizu karaktera ili reči
- redosled karaktera i reči ima značenje
Tekst
- u praksi se tekst često predstavlja kao vektor, gde se za analizu koriste frekvencije reči u dokumentu
- reči se često nazivaju i termima (eng. terms), pa se redosled reči u dokumentu u ovoj reprezentaciji zanemaruje
- za kolekciju od n dokumenata i d terma, pravi se matrica dokumenata i termina (eng. document-term matrix) dimenzija n × d
- atributi predstavljaju reči (termove)
- vrednosti atributa predstavljaju pojavljivanje ili frekvencije tih reči u dokumentu
- asimetrični podaci
Tekst
| Term | Dokument 1 | Dokument 2 | Dokument 3 |
|---|---|---|---|
| data | 2 | 0 | 1 |
| mining | 1 | 1 | 0 |
| model | 0 | 2 | 1 |
| cluster | 1 | 0 | 2 |
Vremenske serije
- vremenske serije sadrže vrednosti koje se obično kontinuirano generišu tokom vremena
- kontinuirano merenje temperature senzorom
- postoji implicitna zavisnost između vrednosti koje se javljaju u različitim trenucima merenja
Vremenske serije
Postoje dve vrste atributa
- kontekstualni atributi
- atributi ponašanja
Vremenske serije
- kontekstualni atributi
- definišu kontekst na osnovu kojeg implicitne zavisnosti nastaju u podacima
- vremenska oznaka (eng. timestamp) u trenutku merenja može se smatrati kontekstualnim atributom
- umesto vremenske oznake može se koristiti pozicija koja određuje redosled merenja
- kod vremenskih serija, obično postoji samo jedan kontekstualni atribut (vreme), dok kod drugih tipova podataka može postojati više kontekstualnih atributa
- kod prostornih podataka kao kontekstualni atributi mogu se koristiti koordinate položaja
Vremenske serije
- atributi ponašanja
- atributi ponašanja predstavljaju vrednosti koje se mere u datom kontekstu
- npr. temperatura predstavlja atribut ponašanja
- može biti i više atributa ponašanja
- npr. više senzora istovremeno meri različite parametre (temperaturu, vlažnost i pritisak) u istim vremenskim trenucima
Diskretne sekvence i niske
- diskretne sekvence mogu se posmatrati kao kategorički ekvivalent vremenskim serijama
- kontekstualni atribut je vremenska oznaka ili pozicija elemenata
- atribut ponašanja je kategoričkog tipa (slova, simboli)
Diskretne sekvence i niske
- npr. biološke sekvence - nizovi nukleotida ili aminokiselina

Mrežni i grafovski podaci
objekti mogu odgovarati čvorovima u mreži, dok odnosi između njih predstavljaju grane koje povezuju čvorove
čvorovi u mreži mogu imati dodeljene atribute, npr. ime korisnika, starost, tip entiteta ili druge karakteristike
fokus analize je najčešće na strukturi povezanosti, tj. odnosima između čvorova, a ne samo na pojedinačnim vrednostima atributa
npr. društvene mreže
Mrežni i grafovski podaci
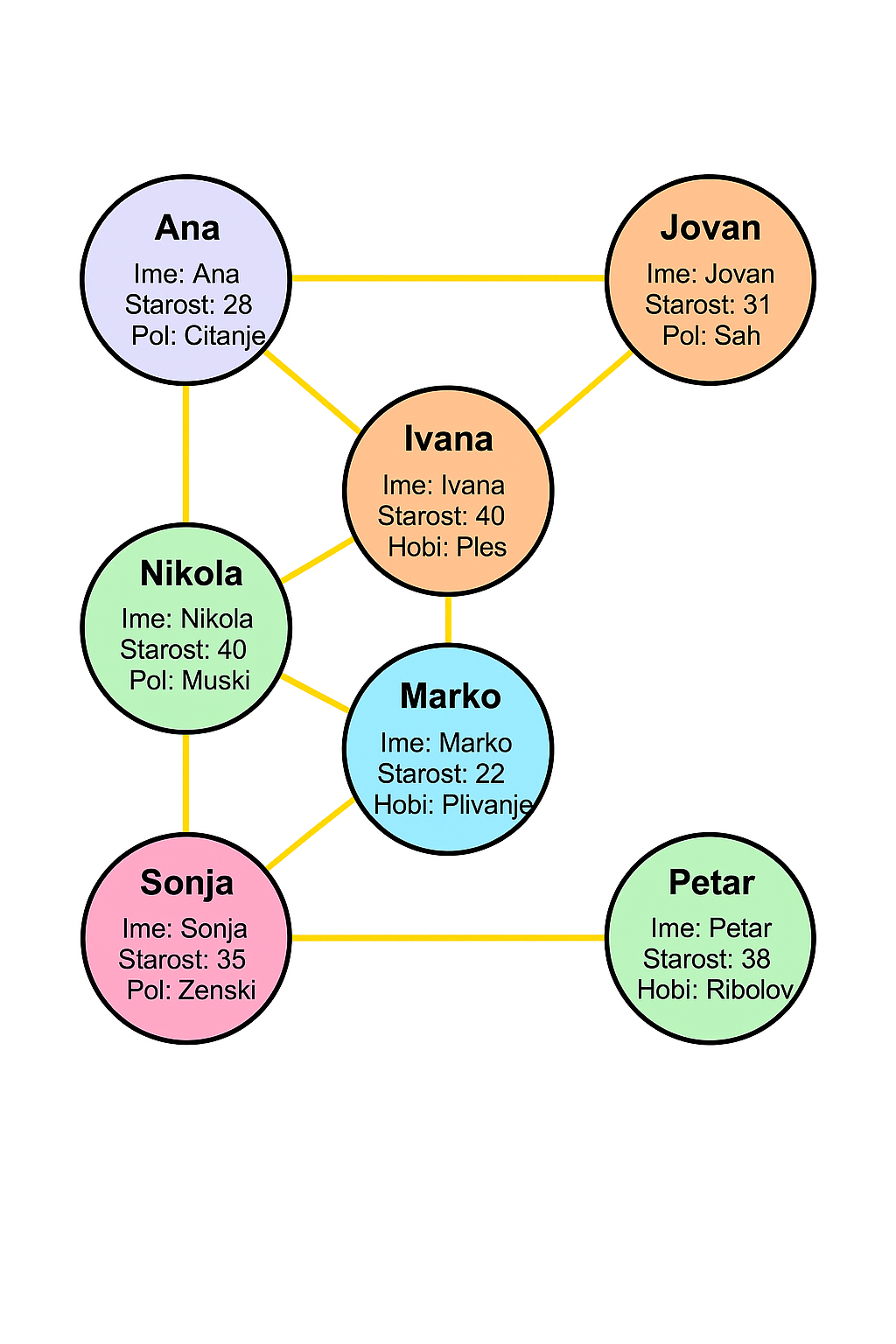
Mrežni i grafovski podaci
- mrežni podaci predstavljaju opštu i fleksibilnu formu reprezentacije
- ova forma se koristiti za rešavanje mnogih zadataka zasnovanih na sličnosti između podataka
- multidimenzionalni podaci mogu se pretvoriti u mrežni oblik tako što se za svaku instancu u bazi podataka pravi čvor, dok se sličnosti između zapisa predstavljaju granama koje povezuju te čvorove
Gradivni blokovi u procesu IP
Tehnike koje se koriste kao gradivni blokovi u procesu IP:
- klasterovanje (eng. clustering)
- klasifikacija (eng. classification)
- pravila pridruživanja (eng. association pattern mining)
- pronalaženje elemenata van granica (eng. outliers)
Gradivni blokovi u procesu IP
- klasterovanje – pronalaženje prirodnih grupa ili klastera u podacima na osnovu njihove sličnosti
- bitno je kako se definiše sličnost
- nenadgledano učenje
Klasterovanje

Gradivni blokovi u procesu IP
- klasifikacija – dodeljivanje unapred definisanih klasa novim instancama na osnovu prethodno naučenih obrazaca
- nadgledano učenje
- ciljni atribut
- trening i test skup
Klasifikacija

Gradivni blokovi u procesu IP
- pravila pridruživanja (eng. association pattern mining) – otkrivanje veza i pravila koja se često pojavljuju zajedno u podacima
- traže se dovoljno česti obrasci ili podskupovi koji se javljaju zajedno
Pravila pridruživanja
- „ako kupac kupi mleko, često kupi i hleb“
- \(Mleko \Rightarrow Hleb\)

Gradivni blokovi u procesu IP
- pronalaženje elemenata van granica (eng. outliers) – identifikovanje neobičnih podataka koji se ne uklapaju u uobičajene obrasce
- npr. visina 220 cm
Pronalaženje elemenata van granica

Vizuelizacija podataka

Izazovi
- zbog različitih tipova podataka često je potrebno razviti prilagođene varijante osnovnih pristupa
- nagli rast količine podataka predstavlja ozbiljan izazov za njihovu obradu
- potok podataka (eng. data stream)
Dijagram procesa istraživanja podataka

Podaci
- Podaci mogu biti iz različitih izvora te su često neusklađene
- Neke vrednosti mogu nedostajati ili biti pogrešne
Priprema podataka
- Primena i uspeh istraživanja podataka u velikoj meri zavise od tehnika pripreme podataka
- Skup atributa podataka ima veći uticaj na kvalitet rezultata nego odabir algoritma
- Priprema podataka zahteva ljudsku intuiciju i stručna znanja iz domena kako bi podaci bili pripremljeni na pravi način
Priprema podataka
- Postoje razne tehnike za pripremu podataka
- Ne postoje pravila koja preciziraju koje tehnike treba primeniti i kojim redosledom za određeni tip problema
- Proces pronalaženja pravih tehnika u većoj meri zavisi od uvida i znanja koji se stiču tokom pripreme podataka i naknadne primene algoritama učenja
Priprema podataka
- Koraci u pripremi podataka:
- Izdvajanje karakteristika od interesa
- Čišćenje podataka - obrada nedostajućih i pogrešnih vrednosti iz podataka
- uklanjanje ili procena
- Transformacija vrednosti atributa
- Smanjenje podataka
Čišćenje podataka
Čišćenje podataka - obrada nedostajućih i pogrešnih vrednosti iz podataka
primer korisničke ankete
Greške nastaju tokom prikupljanja podataka
Neki uzroci su:
- Nepouzdanost senzora
- Namerno ili nenamerno davanje netačnih informacija
- Ručni unos podataka
- Namerno neprikupljanje određenih polja, npr. zbog cene
Predlog za obradu nedostajućih vrednosti?
Rad sa nedostajućim vrednostima
Eliminacija instanci koje sadrže nedostajuće vrednosti
Procena nedostajućih vrednosti (imputacija)
Jednostavna procena:
- srednja vrednost ili medijana za numeričke vrednosti
- najčešća vrednost za kategorijske vrednosti
Rad sa netačnim i nedoslednim vrednostima
- Hot-deck - nedostajuća vrednost zamenjuje se vrednošću koju ima slična instanca (npr. najbliži sused)
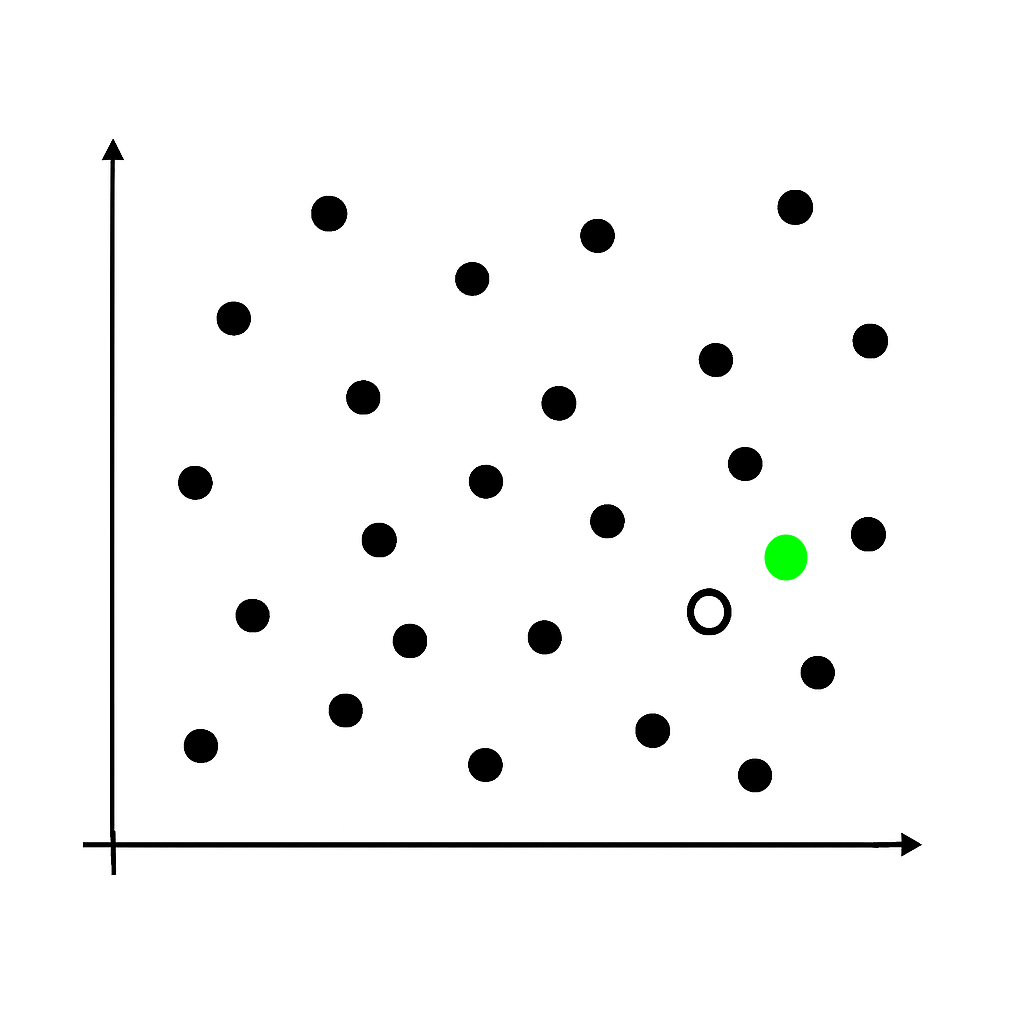
Rad sa netačnim i nedoslednim vrednostima
- Modelske metode, npr.
- kNN - prosek K najbližih suseda
- regresija
Rad sa nedostajućim vrednostima
Greške nastale u procesu imputacije mogu uticati na rezultate algoritama IP
Mogu se birati algoritmi IP koji mogu da rade sa nedostajućim vrednostima
Rad sa nedostajućim vrednostima
- Kod podataka sa zavisnostima, kao što su vremenske serije ili prostorni podaci, za procenu nedostajućih vrednosti koriste se vrednosti atributa ponašanja iz kontekstualno bliskih instanci
- npr. za nedostajuću vrednost može se koristiti prosek vrednosti u vremenskim koracima neposredno pre i posle nedostajuće pozicije
- vrednosti iz poslednjih N vremenskih koraka mogu se linearno interpolirati da bi se dobila procena nedostajuće vrednosti
Rad sa netačnim i nedoslednim vrednostima
- Nekad je potrebno primeniti domensko znanje
- Potrebno je znati:
- očekivane intervale ili moguće vrednosti atributa
- pravila koja definišu odnose između različitih atributa
- Npr. ako je visina osobe 185 cm i težina 15kg
Rad sa netačnim i nedoslednim vrednostima
- Metodi zasnovani na podacima - koristi se statističko ponašanje podataka da bi se otkrili odstupajući unosi
- Odstupajući unosi mogu biti rezultat grešaka pri prikupljanju podataka, ali mogu biti i elementi van granica i imati
- interesantno ili važno ponašanje sistema
- retke, ali validne pojave
- Odstupajući unos mora biti ručno proveren pre nego što se odbaci
Rad sa netačnim i nedoslednim vrednostima
- Statistike
- Medijana (eng. median) - vrednost koja deli slučajeve na pola nakon sortiranja. Ako postoji paran broj slučajeva, medijan je prosek dva srednja slučaja kada se sortiraju po rastućem ili opadajućem redosledu.
Rad sa netačnim i nedoslednim vrednostima
- Statistike
- Postotna vrednost ili percentil za neki izabrani broj p definiše se poštujući uslov da je barem p% vrednosti u skupu manje ili jednako toj vrednosti
- percentil je poznat i kao prvi kvartil (\(Q_1\))
- percentil je medijana ili drugi kvartil (\(Q_2\))
- percentil je poznat i kao treći kvartil (\(Q_3\))
- interkvartilni raspon (\(Q_3 - Q_1\))
- Postotna vrednost ili percentil za neki izabrani broj p definiše se poštujući uslov da je barem p% vrednosti u skupu manje ili jednako toj vrednosti
Rad sa netačnim i nedoslednim vrednostima
- Određivanje elemenata van granica korišćenjem percentila
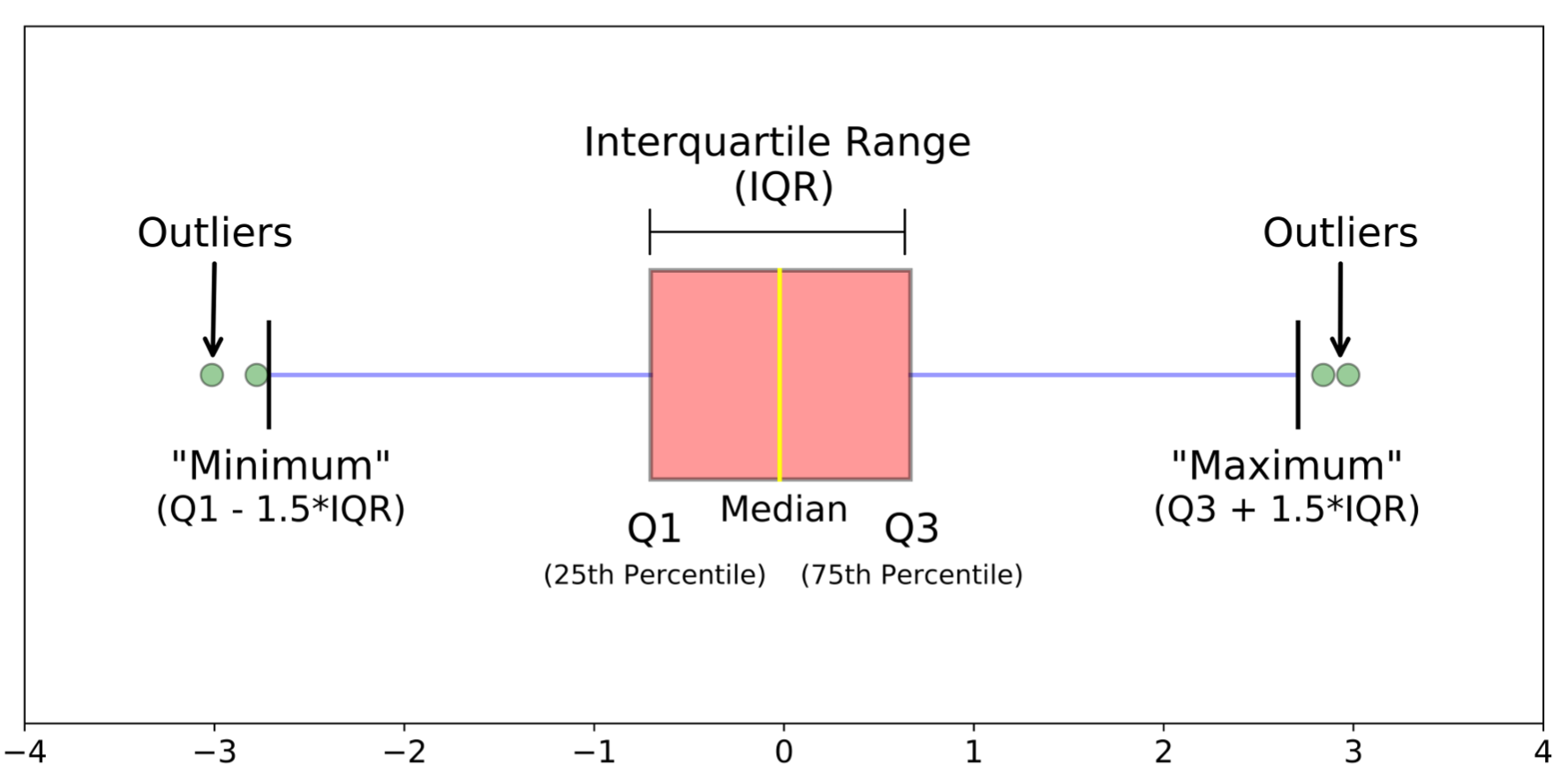
Rad sa netačnim i nedoslednim vrednostima
- Određivanje elemenata van granica metodom standardne devijacije
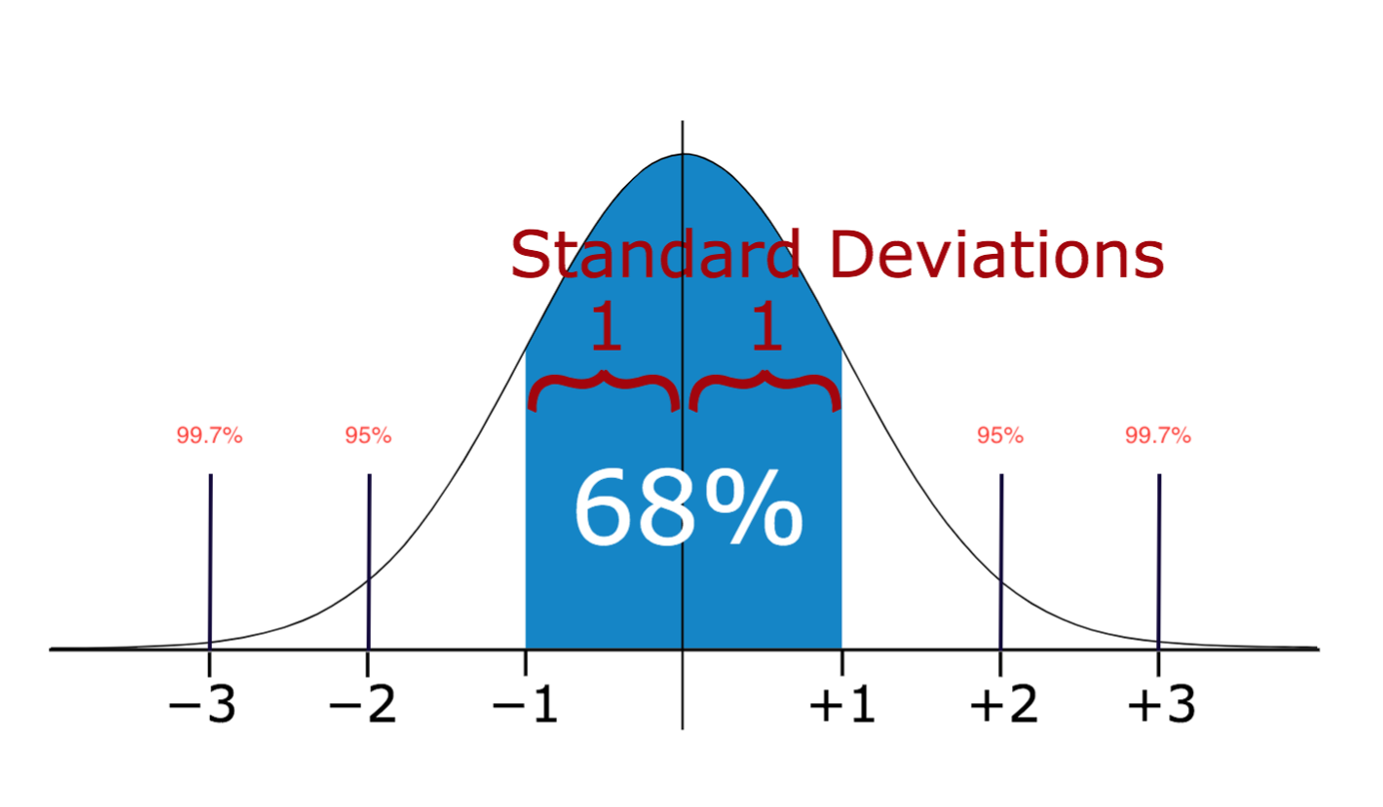
Transformacija vrednosti atributa
- Podaci često sadrže različite tipove atributa
- npr. demografski skup podataka
- pravi problem u izboru algoritma IP
Diskretizacija
- Diskretizacija - pretvaranje numeričkog u kategorijski tip
- Koraci
- podela opsega numeričkih vrednosti na N intervala
- intervalima se dodeljuju kategorijske vrednosti
Npr. vrednosti atributa starost se dele u intervale
\([0,10], [11,20],[21,30]...[100,110]\)
i redom im se dodeljuju vrednosti “1”, “2”, “3” …
- Problemi?
Intervali jednake širine
- Svaki interval \([a, b]\) bira se tako da je \(b − a\) isto za sve intervale
- Da bi se izračunale granice intervala, najpre se odrede minimalna i maksimalna vrednost atributa
- Opseg \([min, max]\) zatim se deli na N intervala jednake dužine
- Npr. starost, visina
- Nedostatak - ne radi dobro za podatke koji su neujednačeno raspoređeni
- npr. atribut plata
Intervali jednake dubine
- Intervali se biraju tako da svaki interval ima približno jednak broj instanci
- Procedura:
- vrednosti atributa se urede
- određuju se granične tačke tako da svaki interval sadrži jednak broj elemenata
- Npr. plate, cene
Intervali jednake logaritamske širine
Svaki interval \([a, b]\) se bira tako da je \(log(b) − log(a)\) isti za sve intervale
Ova vrsta izbora intervala dovodi do toga da se intervali geometrijski povećavaju
- npr: \([a, a • α], [a • α, a • α²]\), itd. za neko \(α > 1\)
Ovakvi intervali su korisni kada atribut ima eksponencijalnu distribuciju
Npr. veličina fajla
Intervali jednake logaritamske širine
- Ako frekventna distribucija atributa može da se opiše nekom funkcijom, prirodan pristup je da se intervali \([a, b]\) biraju tako da je: \(f(b) − f(a)\) konstanta za neku funkciju \(f(•)\)
- ideja je da se funkcija \(f(•)\) izabere tako da svaki interval sadrži približno jednak broj instanci
- U praksi je teško naći takvu funkciju
Binarizacija
- Binarizacija - pretvaranje kategorijskih podataka u binarni oblik
- Ako kategorijski atribut ima N različitih vrednosti onda se kreira N binarnih atributa
- Svaki binarni atribut odgovara jednoj mogućoj vrednosti kategorijskog atributa
- Za svaku instancu:
- tačno jedan od N binarnih atributa dobija vrednost
- svi ostali binarni atributi imaju vrednost 0
Binarizacija
| Instanca | Originalna boja | Plava | Crvena | Zelena |
|---|---|---|---|---|
| 1 | Plava | 1 | 0 | 0 |
| 2 | Zelena | 0 | 0 | 1 |
| 3 | Crvena | 0 | 1 | 0 |
| 4 | Plava | 1 | 0 | 0 |
Mere bliskosti
Neki algoritmi IP kao ulaz koriste samo matricu bliskosti instanci
Blizina (eng. proximity) označava ili sličnost ili različitost
Sličnost
- Numerička mera koliko su dva objekta slična
- Što dva objekta više liče jedan na drugi sličnost im je veća
- često se meri vrednostima u intervalu [0,1]
Mere bliskosti
| A | B | C | D | |
|---|---|---|---|---|
| A | 1.0 | 0.8 | 0.3 | 0.1 |
| B | 0.8 | 1.0 | 0.4 | 0.2 |
| C | 0.3 | 0.4 | 1.0 | 0.7 |
| D | 0.1 | 0.2 | 0.7 | 1.0 |
Mere bliskosti
- Različitost
- Numerička mera koliko su dva objekta različita
- Što dva objekta više liče jedan na drugi različitost im je manja
- Najmanja različitost je često 0; gornja granica varira
- Kao sinonim koristi se i termin rastojanje
Različitost između objekata podataka
Rastojanje Minkovskog:
\(dist= (\sum_{k=1}^n |p_k - q_k|^{r} )^{\frac{1}{r}}\)
gde je
r parametar
n broj dimenzija (atributa)
\(p_k\) i \(q_k\) su vrednosti k. atributa objekata p i q
r=1 Menhetn (L1 norma) rastojanje
r=2 Euklidsko rastojanje
Skaliranje podataka
Različite karakteristike mogu biti na različitim skalama, pa stoga nisu uporedive
npr. plata i starost
Standardizacija \(\frac{x - \mu}{\sigma}\)
- većina standardizovanih vrednosti biće u opsegu [-3, 3], pod pretpostavkom normalne raspodele
Normalizacija \(\frac{x - \min}{\max - \min}\)
- opseg [0, 1]
- nije efikasna kada atribut ima ekstremne vrednosti jer će većina vrednosti biti „sabijena“ u mali opseg
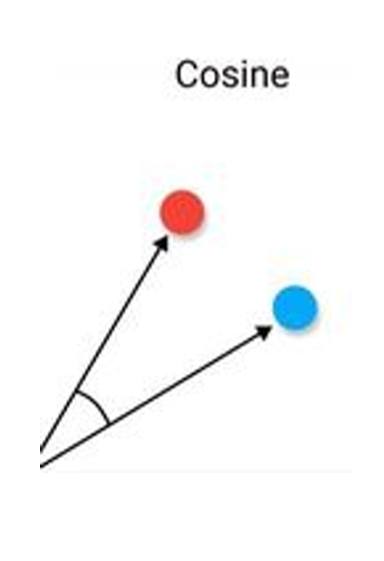
Mere sličnosti
Kosinusna sličnost
\(cos(p,q) = \frac{p \cdot q} {\|p\|\|q\|}\)
- p i q - dva vektora
- \(\cdot\) označava skalarni proizvod vektora
- \(\|d\|\) označava dužinu vektora d
- asimetrični podaci
- najčešća mera sličnosti dokumenata
Mere sličnosti
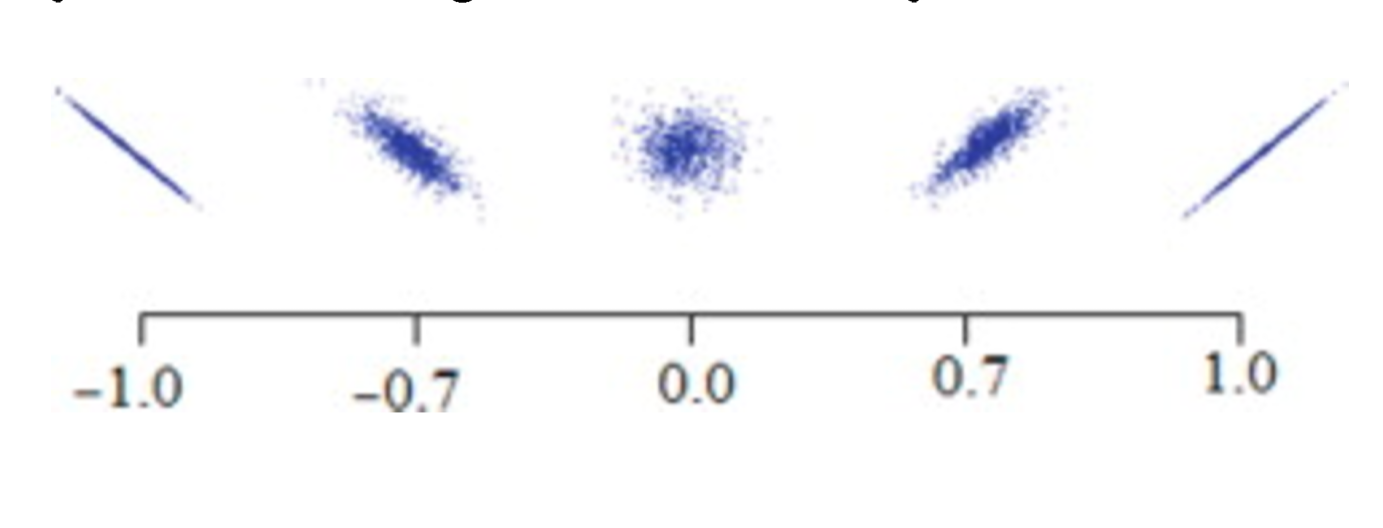
Korelacija
\(r = \frac{kovarijansa(x,y)} {standardna\_devijacija(x)*standardna\_devijacija(y)}\)
- x i y - dva vektora
- korelacija dva objekta koji imaju binarne ili neprekidne atribute je mera linearnog odnosa između njihovih atributa
Mere sličnosti

Smanjenje podataka
- Smanjenje podataka (eng. data reduction)
- Dodavanje većeg broja promenljivih u skup podataka potencijalno obezbeđuje više informacija
- problem: algoritmu postaje teže da obradi podatke
- Smanjenje broja promenljivih je korisno i za izbegavanje preprilagođavanja modela instancama na kojima se trenira (eng. overfitting)
Smanjenje podataka
- Tri tipa tehnika za smanjenje podataka:
- smanjenje broja različitih vrednosti u atributima (eng. value reduction)
- smanjenje broja instanci (eng. case reduction)
- smanjenje broja atributa (dimenzija) (eng. feature reduction)
Smanjenje podataka

Smanjenje broja različitih vrednosti
- Smanjenje broja različitih vrednosti u atributima se postiže grupisanjem više vrednosti u jednu kategoriju
Smanjenje broja različitih vrednosti
| Originalna vrednost | Nova kategorija |
|---|---|
| Softverski inženjer | IT |
| Programer | IT |
| Web developer | IT |
| Data analitičar | IT |
| Profesor | Obrazovanje |
| Nastavnik | Obrazovanje |
| Asistent | Obrazovanje |
| Hirurg | Medicina |
| Medicinska sestra | Medicina |
Smanjenje broja instanci
Smanjenje broja instanci se postiže primenom strategija uzorkovanja
Nepristrasno uzorkovanje - bira se unapred definisani deo (f) podataka koji se zadržava za analizu
Smanjenje broja instanci
- Uzimanje uzorka bez ponavljanja (eng. sampling without replacement)
- Polazi se od skupa D sa n instanci
- Nasumično se bira ⌊n • f⌋ zapisa
- Nema duplikata, osim ako ih ima u originalnim podacima
- Uzimanje uzorka sa ponavljanjem (eng. sampling with replacement)
- Bira se ⌊n • f⌋ zapisa
- Svaki izbor je nezavisan
- Moguće je ponavljanje instanci jer se ista instanca može izabrati više puta
Smanjenje broja instanci
- Pristrasno uzorkovanje (eng. biased sampling)
- Neki delovi podataka imaju veću verovatnoću izbora jer su važniji za analizu
- Npr. vremenske serije - skoriji zapisi imaju veću verovatnoću da budu izabrani, a stariji manju
Smanjenje broja instanci
Stratifikovano uzorkovanje se koristi kada su neke važne grupe u podacima retke, pa ih slučajno uzorkovanje verovatno ne bi obuhvatilo
U uzorku postoji onaj procenat instanci svake grupe koji odgovara procentu instanci te grupe u originalnom skupu
Npr. u istraživanju stanovništva
- uzorak verovatno neće sadržati milijardera (veoma retko)
- stratifikovan uzorak bi izdvojio proporcionalni broj ljudi iz svake grupe prihoda, uključujući i najviše prihode
Izbor podskupa atributa
Izbor podskupa atributa (eng. feature subset selection)
Neki atributi mogu biti uklonjeni kada je poznato da nisu relevantni
Doprinos
- kvalitet ulaznih podataka
- uklanjanje šuma
- smanjenje dimenzionalnosti
- efikasnost algoritama
- poboljšanje preciznosti analiza
Izbor podskupa atributa
- Dva pristupa
- nenadgledani izbor atributa
- nadgledani izbor atributa
Nenadgledani izbor atributa
- Uklanjanje:
- nekorisnih atributa
- redundantnih (višestruko prisutnih ili suvišnih) atributa
- Ne postoje spoljašnji kriterijumi za validaciju koliko je dobro (npr. oznake klase)
- Povezani sa klasterovanjem
Nadgledani izbor atributa
- Nadgledani izbor atributa je relevantna za problem klasifikacije
- Relevantne su samo one karakteristike koje efikasno predviđaju klasu
- Metode za izbor karakteristika često su tesno integrisane sa analitičkim metodama za klasifikaciju
Pregled metoda za izbor podskupa atributa
- Filter metode
- Atributi se procenjuju nezavisno od modela
- Svaki atribut dobija skor na osnovu statističkih ili mera sličnosti
- Često daju slabije rezultate u modelima
Pregled metoda za izbor podskupa atributa
- Metoda zasnovana na varijansi
- Izračuna varijansu svakog atributa
- Ako je varijansa:
- ~0 atribut ima skoro istu vrednost u svim redovima te on ne doprinosi modelu i biće uklonjen
Pregled metoda za izbor podskupa atributa
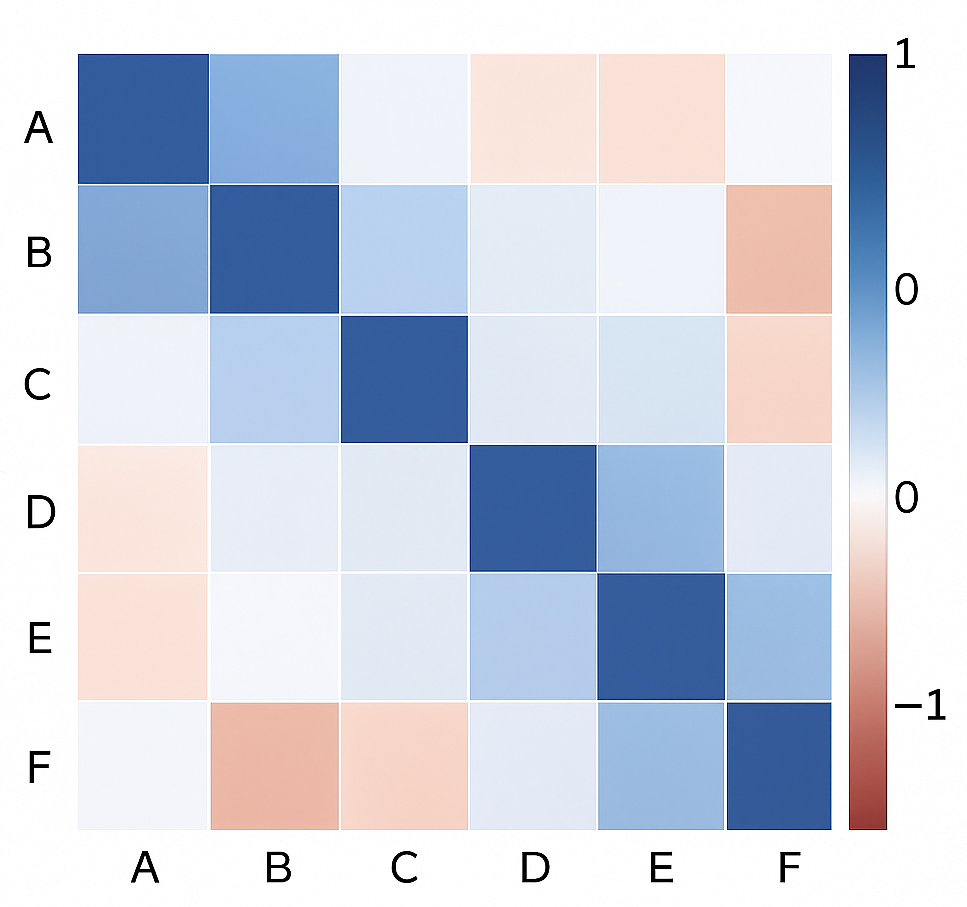
- Metoda zasnovana na korelaciji
- uklanja atribute koji su visoko korelisani
- zadržava jedan atribut od visokokorelisanih i to obično onaj koji
- ima veću varijansu (u nenadgledanim učenjima)
- ima veću korelaciju sa ciljnim atributom (u nadgledanim učenjima)
- je domenski važniji
Primer matrica korelacije
Pregled metoda za izbor podskupa atributa
- Wrapper metode
- Model se više puta trenira sa različitim podskupovima karakteristika
- Kvalitet podskupa se meri na osnovu performansi modela
- Nisu pogodne za velike skupove
Pregled metoda za izbor podskupa atributa
- Embedded metode
- Izbor atributa se vrši tokom treniranja modela
- Model sam određuje važnost atributa, ne zahteva ručno testiranje podskupova
- Vezane za konkretan model
- Neki modeli nemaju podršku za određivanje značajnosti atributa
- Drveta odlučivanja
Literatura
- Charu C. Aggarwal: Data Mining The Textbook, Springer, 2015.
- glava 2
Smanjenje podataka
- Smanjenje podataka (eng. data reduction)
- Dodavanje većeg broja promenljivih u skup podataka potencijalno obezbeđuje više informacija
- Problem - algoritmu postaje teže da obradi podatke
- prokletstvo dimenzionalnosti
- Smanjenje broja promenljivih je korisno i za izbegavanje preprilagođavanja modela instancama na kojima se trenira (eng. overfitting)
Smanjenje podataka
- Cilj je da se obezbedi proces IP koji će proizvesti isti (ili skoro isti) rezultat kada se primeni na redukovanim podacima umesto na originalnim podacima, a da istovremeno proces IP postane efikasniji
Smanjenje podataka
- Tri tipa tehnika za smanjenje podataka:
- smanjenje broja različitih vrednosti u atributima (eng. value reduction)
- smanjenje broja instanci (eng. case reduction)
- smanjenje broja atributa (dimenzija) (eng. feature reduction)
Smanjenje podataka

Smanjenje podataka
- Smanjenje broja atributa (dimenzija) može se izvršiti pomoću transformacije ili projektovanja originalnih podataka u manji prostor
PCA
- Analiza glavnih komponenti
- eng. Principal Components Analysis (PCA)
- Ideja: pronaći skup linearnih transformacija originalnih atributa koji mogu opisati većinu varijanse koristeći manji broj atributa
PCA
- Transformacija se zasniva na pretpostavci da visoka informativnost odgovara visokoj varijansi
- Traži se k ortogonalnih linearnih kombinacija originalnih atributa koje imaju najveću varijansu, pri čemu važi k ≤ n
- Novi skup atributa je uređen po važnosti opadajuće -Preciznije, skup n-dimenzionalnih vektorskih uzoraka \(X=\{x_1, x_2, x_3, \ldots, x_m\}\) treba transformisati u drugi skup \(Y=\{y_1, y_2, \ldots, y_m\}\) iste dimenzionalnosti, ali tako da skup \(Y\) ima osobinu da je najveći deo informacija sadržan u prvih nekoliko dimenzija
PCA
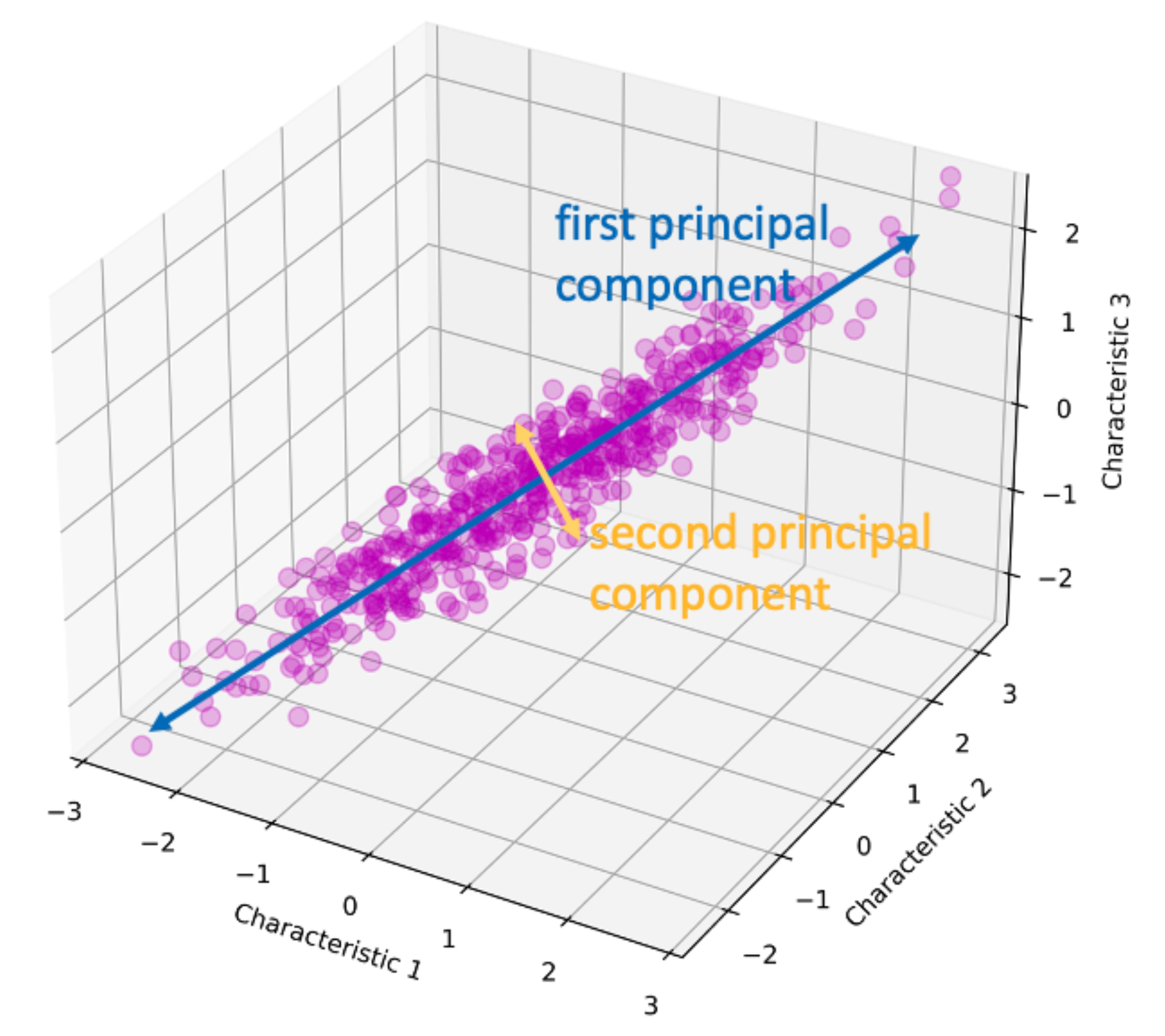
PCA
- Izračunava se \(𝑆\) matrica kovarijansi
\[S=PΛP^T\]
- Kolone matrice 𝑃 sadrže ortonormirane sopstvene vektore matrice S, a Λ je dijagonalna matrica koja sadrži nenegativne sopstvene vrednosti.
- Element \(Λ_{ii}\) predstavlja sopstvenu vrednost koja odgovara i. sopstvenom vektoru (tj. i. koloni matrice P).
- Sopstvene vrednosti predstavljaju varijanse podataka duž odgovarajućih sopstvenih vektora.
PCA
Potrebno je izračunati sopstvene vrednosti matrice kovarijansi \(𝑆\)
Sopstvene vrednosti matrice \(S_{nxn}\) su \(𝜆_1, 𝜆_2, … ,𝜆_𝑛\), pri čemu važi \(𝜆_1 \geq 𝜆_2\geq … \geq 𝜆_𝑛 \geq 0\)
Sopstveni vektori \(𝑒_1,e_2,...,e_n\) odgovaraju sopstvenim vrednostima \(𝜆_1, 𝜆_2, … ,𝜆_𝑛\) i nazivaju se glavne ose ili glavne komponente
PCA
- Glavne ose predstavljaju nove, transformisane ose n-dimenzionalnog prostora, u kojem su novi atributi međusobno nekorelisani, a varijansa i-te komponente jednaka je i-toj svojstvenoj vrednosti
- Pošto su \(𝜆_1 \geq 𝜆_2\geq … \geq 𝜆_𝑛\) poređane po veličini, najveći deo informacija o skupu podataka koncentrisan je u prvih nekoliko glavnih komponenti
PCA
Originalni skup D u transformisani skup D* se računa sa
\[D^*=𝐷𝑃\]
Iako je transformisana matrica podataka 𝐷* iste dimenzije kao matrica D, prvih m≤n kolona pokazaće značajnu varijaciju u vrednostima.
PCA
- Koliko glavnih komponenti je potrebno da bi se podaci dobro predstavili?
- Ako se podeli zbir prvih m sopstvenih vrednosti sa zbirom svih varijansi (tj. svih sopstvenih vrednosti), dobija se mera kvaliteta reprezentacije zasnovane na prvih m glavnih komponenti \[ R= \frac{\sum_{i=1}^m \lambda_i}{\sum_{i=1}^n \lambda_i}\]
- Rezultat se izražava u procentima, i ako projekcija obuhvata više od 90% ukupne varijanse, smatra se dobrom
PCA
Osnovna procedura:
- Normalizovati ulazne podatke kako bi se izjednačili opsezi atributa
- Izračunati m ortonormiranih vektora koji čine bazu za normalizovane ulazne podatke - glavne komponente.
- Sortirati glavne komponente prema pripadajućim sopstvenim vrednostima
- Originalni podaci se izražavaju kao linearne kombinacije glavnih komponenti
- Smanjiti podatke uklanjanjem slabijih komponenti, tj. onih sa malom varijansom
PCA
- PCA se često koristi kao alat za vizualizaciju podataka, tako što se višedimenzionipodaci redukuju na 2D ili 3D podatke
- Pretpostavlja linearnu strukturu
- Komponente su teško interpretabilne (npr. u genomici)
- Osetljiv na skaliranje i elemente van granica
SVD
- Singularna dekompozicija
- Singular Value Decomposition (eng. SVD)
SVD
SVD se može definisati kao rastavljanje matrice na proizvod tri matrice:
\[D=QΣP^T\]
Gde je:
D matrica podataka dimenzije \(𝑛×d\)
Q matrica dimenzije \(𝑛×𝑛\) sa ortonormalnim kolonama (levi singularni vektori)
Σ matrica dimenzije \(𝑛×𝑑\), dijagonalna, sadrži nenegativne singularne vrednosti poređane neopadajućim redosledom
P matrica dimenzija \(d×d\) sa ortonormalnim kolonama (desni singularni vektori)
SVD
- Iako je Σ pravougaona, naziva se dijagonalnom jer su jedini nenula elementi oblika \(Σ_{ii}\)
- Broj nenula dijagonalnih elemenata matrice Σ je \(\min(n,d)\)
- Zbog ortonormalnosti: \[𝑃^𝑇𝑃=𝐼, 𝑄^𝑇𝑄=𝐼\]
Osobine SVD
Kolone matrice Q (levi singularni vektori) jesu ortonormalni sopstveni vektori matrice \(𝐷𝐷^𝑇\)
Zaista:
\[𝐷𝐷^𝑇=𝑄Σ(𝑃^𝑇𝑃)Σ^𝑇𝑄^𝑇=𝑄ΣΣ^𝑇𝑄^𝑇\]
Kvadrati nenula singularnih vrednosti (dijagonalni elementi \(ΣΣ^𝑇\) ) jesu sopstvene vrednosti matrice \(DD^T\)
Osobine SVD
- Kolone matrice P (desni singularni vektori) jesu ortonormalni sopstveni vektori matrice \(𝐷^𝑇𝐷\)
- Kvadrati nenula singularnih vrednosti (dijagonalni elementi \(Σ^𝑇Σ\)) jesu sopstvene vrednosti matrice \(𝐷^𝑇𝐷\)
- Nenula sopstvene vrednosti \(𝐷^𝑇𝐷\) i \(𝐷𝐷^𝑇\) su iste
- Desni singularni vektori predstavljaju bazne vektore analogne sopstvenim vektorima kovarijacione matrice u PCA
Veza SVD i PCA
- Matrica kovarijansi centriranih podataka glasi:
\[\frac{𝐷^𝑇𝐷}{n}\]
i desni singularni vektori SVD-a su sopstveni vektori \(𝐷^𝑇𝐷\) stoga
sopstveni vektori PCA identični su desnim singularnim vektorima SVD-a za centrirane podatke
kvadrati singularnih vrednosti jednaki su \(n\) puta sopstvenim vrednostima PCA
Veza SVD i PCA
- Zato SVD i PCA daju istu transformaciju za standardizovane podatke
Skraćena SVD
Skraćena SVD - metoda aproksimacije matrice
Neka su singularne vrednosti u Σ poređane opadajuće
Neka su:
- \(𝑃_𝑘\) prvih 𝑘 kolona matrice 𝑃
- \(𝑄_𝑘\) prvih 𝑘 kolona matrice 𝑄
- \(Σ_𝑘\) kvadratna matrica \(𝑘×𝑘\) sa najvećim singularnim vrednostima
Tada:
\[𝐷 ≈ 𝑄_kΣ_𝑘𝑃_𝑘^𝑇 \]
Skraćena SVD
- Kolone matrice \(𝑃_𝑘\) predstavljaju k-dimenzioni bazni sistem za redukovanu reprezentaciju podataka
- Redukovani podaci su:
\[𝐷_𝑘=𝐷𝑃_𝑘=𝑄_𝑘Σ_𝑘\]
- Svaki od 𝑛 redova matrice \(𝐷_k\) sadrži 𝑘 koordinata transformisane tačke u novom koordinatnom sistemu
- Obično je: 𝑘≪𝑛, 𝑘≪𝑑
SVD
- Opštiji od PCA (radi i bez centriranja podataka)
- Efikasan za velike i retke matrice
- Može biti računarski skup za ogromne matrice
t-SNE
- t-Distributed Stochastic Neighbor Embedding (t-SNE)
- Stohastičko mapiranje suseda zasnovano na t-raspodeli (t-SNE)
- Metoda redukcije dimenzionalnosti koja pretvara visokodimenzionalni skup podataka \(X = \{x_1, x_2, \ldots, x_n\}\) u dvodimenzionalne ili trodimenzionalne podatke \(Y=\{y_1, y_2, \ldots, y_n\}\) koji se mogu prikazati na dijagramu rasipanja (eng. scatterplot)
t-SNE
- Cilj redukcije dimenzionalnosti jeste da se u mapiranju niske dimenzionalnosti sačuva što je moguće više značajne strukture visokodimenzionalnih podataka
- t-SNE je u stanju da veoma dobro očuva veliki deo lokalne strukture visokodimenzionalnih podataka, a istovremeno otkriva i globalnu strukturu, kao što je postojanje klastera
- U 2D mapiranju tačke iz istih klastera primetno su bliže jedna drugoj u poređenju sa tačkama iz različitih klastera
t-SNE
- Euklidska rastojanja u višedimenzionom prostoru između tačaka se pretvaraju u uslovne verovatnoće koje predstavljaju sličnost
- Sličnost podatka \(x_j\) u odnosu na podatak \(x_i\) je uslovna verovatnoća \(𝑝_{ј|i}\), koja predstavlja verovatnoću da bi \(x_i\) izabrao \(x_j\) za svog suseda kada bi se susedi birali proporcionalno gustini verovatnoće određene Gausovom raspodelom centriranom u \(x_i\)
t-SNE
- Za tačke koje su blizu jedna drugoj, vrednost \(𝑝_{ј|i}\) je relativno velika, dok je za tačke koje su međusobno udaljene vrednost praktično zanemarljiva
\[𝑝_{ј|i} =\frac{\exp(-||x_i-x_j||^2/2\sigma_i^2)}{\sum_{k\neq i}\exp(-||x_i-x_k||^2/2\sigma_i^2)}\]
—
t-SNE
- Ne postoji jedna jedina vrednost \(\sigma_i\) koja je optimalna za sve tačke u skupu podataka
- Gustina podataka se obično razlikuje u različitim regionima prostora
- U gustim regionima obično je pogodnija manja vrednost za \(\sigma_i\), dok su u ređim regionima veće vrednosti
—
t-SNE
Svaka vrednost \(\sigma_i\) određuje raspodelu verovatnoće \(P_i\) nad svim ostalim tačkama
Ova raspodela ima entropiju koja raste kako \(\sigma_i\) raste
SNE vrši binarnu pretragu kako bi pronašao vrednost \(\sigma_i\) koja daje raspodelu \(P_i\) sa fiksnom perpleksnošću (ebg. perplexity), vrednošću koju zadaje korisnik
—
t-SNE
- Perpleksnost je definisana kao: \[Perp(𝑃_𝑖)=2^{𝐻(𝑃_𝑖)}\]
gde je \(𝐻(𝑃_i)\) Šenonova entropija raspodele \(𝑃_i\), izražena u bitovima:
\[𝐻(𝑃_𝑖)=−\sum_j 𝑝_{𝑗∣𝑖}log_2 𝑝_{𝑗∣𝑖}\]
Perplexity se može tumačiti kao mera efektivnog broja suseda, a uobičajene vrednosti su između 5 i 50.
mala perpleksnost - fokus na lokalnu strukturu (bliske tačke)
velika perpleksnost - fokus na širu, globalniju strukturu
—
t-SNE

t-SNE
Kada se zada vrednost perpleksnost parametra, algoritam sam bira odgovarajuće vrednosti \(\sigma_i\) tako što ih pronalazi binarnom pretragom
Sličnosti između podataka u prostoru niske dimenzionalnosti se određuju na sličan način, s tim što se umesto Gausove raspodele koristi Studentova t-raspodela sa jednim stepenom slobode
t-SNE koristi Studentovu t-raspodelu u niskoj dimenziji jer njeni repovi omogućavaju da udaljene tačke ostanu dovoljno razdvojene, čime se rešava problem zbijanja (eng. crowding) i poboljšava vizuelno odvajanje klastera
—
t-SNE
Ako tačke na mapi \(𝑦_𝑖\) i \(𝑦_𝑗\) pravilno modeluju sličnost između visokodimenzionalnih tačaka \(𝑥_i\) i \(𝑥_j\), tada će uslovne verovatnoće \(𝑝_{𝑗∣i}\) i \(q_{𝑗∣i}\) biti jednake
t-SNE traži reprezentaciju podataka u prostoru niske dimenzionalnosti koja minimizuje nepodudaranje između \(𝑝_{𝑗∣i}\) i \(q_{𝑗∣i}\)
\(p_{ij} = \frac{p_{j|i}+p_{i|j}}{2n}\)
\(q_{ij} =\frac{\exp(-||y_i-y_j||^2)}{\sum_{k\neq i}\exp(-||y_i-y_k||^2)}\)
Mera vernosti kojom \(q_{ij}\) modeluje \(𝑝_{ij}\) je Kulbak-Lajblerova (eng. Kullback–Leiblerova, KL) divergencija
—
t-SNE
Funkcija troška C je \[C= \sum_𝑖 KL(𝑃∥𝑄)=\sum_𝑖 \sum_j 𝑝_{ij} \log \frac{𝑝_{ij}}{q_{ij}}\]
\(𝑃\) zajednička raspodela verovatnoće u visokodimenzionalnom prostoru
\(𝑄\) zajednička raspodela verovatnoće u niskodimenzionalnom prostoru
Mera koliko se model raspodele verovatnoće Q razlikuje od raspodele verovatnoće P
t-SNE
- Cilj je minimizovati zbir KL divergencija preko svih tačaka koristeći metod gradijentnog spusta
- KL-divergencija u t-SNE meri koliko mapa greši u repliciranju lokalnih susedstava iz visokodimenzionalnog prostora
- Najstrože kažnjava greške kod bliskih tačaka, tj. ako je nešto blizu u originalu, ali nije blizu u mapi, kazna je velika
t-SNE
- Odlična vizuelizacija visokodimenzionalnih podataka u 2D/3D
- Otkriva nelinearne strukture i lokalne klastere
- Rezultati zavise od hiperparametara
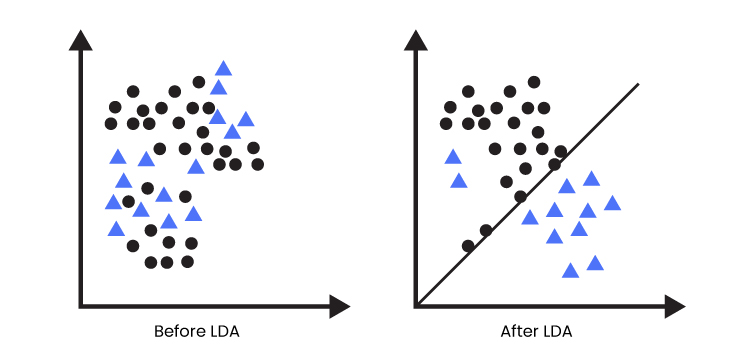
LDA
- Linearna diskriminantna analiza (LDA)
- eng. Linear discriminant analysis
- Metoda koja poboljšava izražajnost atributa radi bolje klasifikacije
- Maksimizuje međuklasne varijanse i minimizuje unutarklasne varijanse
LDA
- Sastoji se od tri faze:
- izračunavanje međuklasne varijanse
- izračunavanja unutarklasne varijanse
- učenje potprostora niže dimenzionalnosti
Koraci LDA
- Standardizacija podataka radi ublažavanja efekata elemenata van granica i šumova.
Koraci LDA
- Izračunavanje međuklasne varijanse
- Pretpostavimo da je originalna matrica podataka \(𝑋= {𝑥_1,𝑥_2,…,𝑥_𝑛} ∈ 𝑅 𝑚×𝑛\) podeljena na skup klasa \(𝑁={𝐶_1,𝐶_2,…,𝐶_𝑁}\). gde je m broj atributa, a n ukupan broj instanci.
Ako je broj uzoraka u c-toj klasi jednak \(𝑛_𝑐\) , tada se vektor srednje vrednosti klase \(𝑀_c\) i ukupna srednja vrednost svih instanci 𝑀 izračunavaju kao:
\[𝑀_𝑐 = \frac{1}{𝑛_𝑐} \sum_{j=1}^{n_c}x_j \] \[𝑀 = \frac{1}{𝑛} \sum_{i=1}^{n}x_i \]
Koraci LDA
Međuklasna matrica predstavlja ukupnu međuklasnu varijansu:
\[ 𝑆_𝐵 = \sum_{𝑖=1}^{𝑁}n_i*(M_i-M)(M_i-M)^T \]
Koraci LDA
- Izračunavanje unutarklasne varijanse
Određuje rastojanje između srednje vrednosti klase i pojedinačnih instanci te klase
Unutarklasna matrica svih klasa se računa kao:
\[𝑆_𝑊 = \sum_{𝑖=1}^{𝑁} \sum_{𝑗∈𝐶_𝑖}(𝑥_j−𝑀_𝑖)*(𝑥_𝑗−𝑀_i)^𝑇\]
Koraci LDA
- Konstrukcija potprostora niže dimenzionalnosti
Određivanje projektivne matrice koja maksimizuje međuklasnu varijansu, a minimizuje unutarklasnu varijansu
Umesto da se optimizuju odvojeno, njihov odnos se maksimizuje
Matrica se pronalazi korišćenjem Fišerovog kriterijuma / rešavanjem optimizacionog problema
\[𝑊=\arg\max_{W} \frac{W^T S_B W}{W^T S_W W}\]
Koraci LDA
Izračunavaju se sopstvene vrednosti \(𝜆 ={𝜆_1,𝜆_2,…,𝜆_𝑚}\) i sopstveni vektori \(𝑉={𝑉_1,𝑉_2,…,𝑉_𝑚}\) matrice \(𝑊=𝑆_𝑊^{−1}𝑆_𝐵\)
Bira se K najvećih sopstvenih vektora, koji formiraju potprostor niže dimenzionalnosti
LDA
LDA
- LDA zahteva linearno separabilne klase, što se može prevazići primenom kernel funkcije
Literatura
Charu C. Aggarwal: Data Mining The Textbook, Springer, 2015.
- glava 2
Zhao, S., Zhang, B., Yang, J. et al. Linear discriminant analysis. Nat Rev Methods Primers 4, 70 (2024). https://doi.org/10.1038/s43586-024-00346-y
Laurens van der Maaten and Geoffrey Hinton. isualizing Data using t-SNE. Journal of Machine Learning Research (2008), pp. 2579-2605. http://jmlr.org/papers/v9/vandermaaten08a.html
Mehmed Kantardzic: Data mining: Concepts, Models, Methods, and Algorithms, 3rd. ed., John Wiley & Sons 2020